虚数与旋转 | HyperPlane

虚数与旋转

发表于 | 更新于 | 阅读次数：

简单解释一下虚数和旋转的关系

平面旋转

将平面上的点(x,y)(x,y)用复数x+yix + yi表示，其中i2=−1i^2 = -1。在这个坐标系中，基为{1,i}\{1, i\}。如果将复平面旋转角度θ\theta，我们可以将11和ii映射到

1→cos⁡θ+isin⁡θi→−sin⁡θ+icos⁡θ\begin{aligned} 1 \rightarrow \cos \theta + i \sin \theta \\ i \rightarrow - \sin \theta + i \cos \theta \end{aligned}

这个应该比较容易验证，在坐标系上画一下就行了。
那么对于一般的坐标来讲呢？我们可以得到

x(cos⁡θ+isin⁡θ)+y(−sin⁡θ+icos⁡θ)=x(cos⁡θ+isin⁡θ)+iy(isin⁡θ+cos⁡θ)=(x+iy)(cos⁡θ+isin⁡θ)=(x+iy)eiθ\begin{aligned} &x(\cos \theta + i \sin \theta) + y (-\sin \theta + i \cos \theta)\\ =& x(\cos \theta + i \sin \theta) + i y ( i\sin \theta + \cos \theta) \\ =& (x + iy) (\cos \theta + i \sin \theta) \\ =& (x + iy) e^{i\theta} \end{aligned}

这里的eiθe^{i\theta}就可以表示旋转，而且左乘右乘也没有什么区别，因为复数乘法有交换律。eiθe^{i\theta}应该也属于李群，有兴趣的朋友可以自己证明一下，这个应该比较简单。同样的θ\theta也就是对应的李代数啦。个人认为使用复数形式来表示旋转比矩阵形式表示旋转看起来直观方便的多。

3D旋转

四元数是拥有3个虚部的复数，单位四元数通常用来表示3D空间中的旋转，和平面旋转大致可以类比一下。ii是复数的虚部，令u\mathbf{u}为纯单位四元数，那么u\mathbf{u}可以表示为某一个通过原点的轴。那么我们有

euθ=cos⁡θ+usin⁡θe^{\mathbf{u}\theta} = \cos \theta + \mathbf{u} \sin \theta

同样的，这样的单位四元数用来表示3D旋转。
但是熟悉单位四元数表示旋转的同学应该都知道使用四元数进行旋转远远不是这么简单，所以我们进行接下来都一些推导。
先让我们脱离四元数，从三维坐标来考虑这个问题吧。元素x\mathbf{x}绕通过原点的轴u\mathbf{u}旋转了角度ϕ\phi。如图
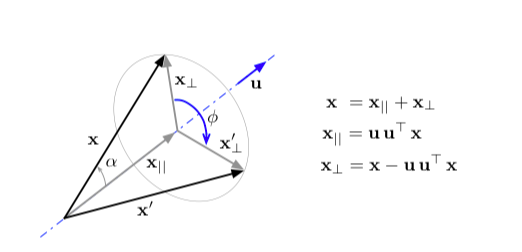
rotation1
其中x∥\mathbf{x}_{\parallel}为与轴u\mathbf{u}平行的分量，x⊥\mathbf{x}_{\perp}为与旋转轴垂直的分量，具体的表示图里有里我就不写了。
接下来要说明的是与轴平行的分量在旋转中是不变的，变化的只有与旋转轴垂直的分量。令x′\mathbf{x}'为x\mathbf{x}旋转后的量，x⊥′\mathbf{x}'_{\perp}为旋转后的垂直分量。在旋转轴u\mathbf{u}的作用下，垂直分量x⊥\mathbf{x}_{\perp}的旋转过程发生在基{x⊥,u×x⊥}\{ \mathbf{x}_{\perp}, \mathbf{u} \times \mathbf{x}_{\perp} \}张成的平面上。回忆一下平面旋转，基为{1,i}\{1,i\}时，旋转角度θ\theta，有

1→cos⁡θ+isin⁡θ1 \rightarrow \cos \theta + i \sin \theta

同样的，我们可以得到

x⊥→x⊥cos⁡ϕ+(u×x⊥)sin⁡ϕ\mathbf{x}_{\perp} \rightarrow \mathbf{x}_{\perp} \cos \phi + (\mathbf{u} \times \mathbf{x}_{\perp}) \sin \phi

最后我们得到旋转后的结果

x′=x∥+x⊥cos⁡ϕ+(u×x⊥)sin⁡ϕ\mathbf{x}' = \mathbf{x}_{\parallel} + \mathbf{x}_{\perp} \cos \phi + (\mathbf{u} \times \mathbf{x}_{\perp}) \sin \phi

根据四元数乘法
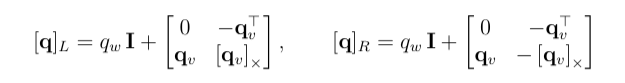
rotation2
我们有

[euθ]L[e−uθ]R=[100cos⁡2θ+sin⁡2θ[u]×+(uuT+[u]×[u]×)sin⁡2θ][e^{\mathbf{u}\theta}]_L [e^{-\mathbf{u}\theta}]_R = \begin{bmatrix} 1 & 0 \\ 0 & \cos^2 \theta + \sin2\theta [\mathbf{u}]_{\times} + (\mathbf{uu}^T + [\mathbf{u}]_{\times}[\mathbf{u}]_{\times})\sin^2\theta \end{bmatrix}

用这个矩阵左乘(0,x)(0, \mathbf{x})可以得到

xcos⁡2θ+sin⁡2θ[u]×x+(uuTx+[u]×[u]×x)sin⁡2θ=xcos⁡2θ+(u×x⊥)sin⁡2θ+(uuTx∥+[u]×[u]×x⊥)sin⁡2θ=xcos⁡2θ+(u×x⊥)sin⁡2θ+x∥sin⁡2θ−x⊥sin⁡2θ=x∥+x⊥cos⁡2θ+(u×x⊥)sin⁡2θ\begin{aligned} &\mathbf{x} \cos^2 \theta + \sin2\theta [\mathbf{u}]_{\times} \mathbf{x} + (\mathbf{uu}^T \mathbf{x} + [\mathbf{u}]_{\times}[\mathbf{u}]_{\times}\mathbf{x})\sin^2\theta \\ = &\mathbf{x} \cos^2 \theta + (\mathbf{u} \times \mathbf{x}_{\perp}) \sin2\theta + (\mathbf{uu}^T \mathbf{x}_{\parallel} + [\mathbf{u}]_{\times}[\mathbf{u}]_{\times}\mathbf{x}_{\perp})\sin^2\theta \\ = & \mathbf{x} \cos^2 \theta + (\mathbf{u} \times \mathbf{x}_{\perp}) \sin2\theta + \mathbf{x}_{\parallel} \sin^2\theta - \mathbf{x}_{\perp} \sin^2\theta \\ = & \mathbf{x}_{\parallel} + \mathbf{x}_{\perp}\cos2\theta + (\mathbf{u} \times \mathbf{x}_{\perp}) \sin2\theta \end{aligned}

所以使用对偶四元数旋转的时候是

euθ/2⊗x⊗e−uθ/2e^{\mathbf{u}\theta/2} \otimes \mathbf{x} \otimes e^{-\mathbf{u}\theta/2}

其中⊗\otimes为四元数乘法。

NOTE：很遗憾，目前为止也只是抽象推导了四元数旋转，还是没有对四元数旋转得到更加直观的理解。3D旋转与虚数的关系并没有2D来的那么直观。相关理解可能后续有时间再继续进行吧。

参考文献

[1]B. V. Adorno, “Robot Kinematic Modeling and Control Based on Dual Quaternion Algebra—Part I: Fundamentals.,” 2017.

[2]J. Sola, “Quaternion kinematics for the error-state KF,” p. 73.