DDG（离散微分几何）：组合曲面

翻译自 DISCRETE DIFFERENTIAL GEOMETRY: AN APPLIED INTRODUCTION 第二章 Combinatorial Surfaces。如果有翻译错误或者不当的地方希望能指出，谢谢～

“Everything should be made as simple as possible, but no simpler.” – Albert Einstein

粗略来讲，曲面（surface）就是一个形状的”外壳/皮“；比如，你可以将一个橙子看作是一个固态球，它的皮可以看作是球状的曲面（尤其当我们将皮考虑为没有厚度的情况）。在我们的日常生活中遇到的各种不同的东西都拥有不同曲面所表示的边界。比如，覆盖甜甜圈的糖浆更像是一个圆环（torus）而不是球。（希望对橙子和甜甜圈讨论能让你对一些几何知识感到“饥饿”。。。HAHAHAHAHA）作为将要真正开始了解曲面微分几何的前奏，我们将由一些很容易从纯粹离散观点理解的对象开始，即组合曲面（combinatorial surfaces），或者说形状的描述仅仅告诉你曲面是如何连接的（connected up）而不告诉你它们在空间的哪个位置（where they are in space）。在离散微分几何中，组合曲面有效扮演了拓扑曲面（topological surfaces）在平滑设置中同样的角色。在这份笔记中我们不会深入到拓扑学，但是在“没有几何（sans geometry）的情况下”使用离散曲面的时候应该能对于拓扑学是讨论什么的给你足够好的感觉。具体而言，我们将讨论几种方法来编码组合曲面的连接：抽象单纯复形（abstract simplicial complex），邻接矩阵（adjacency matrices）和半边网格（halfedge mesh），所有内容都和我们之后要使用的更加丰富的几何对象和算法联系在一起。

在爱因斯坦的提示下，我们将对形状长什么样做一些简单假设，同时仍然保留足够的灵活性去描述在自然世界中能发现的各种对象。这种简化不止能让建立明确几何现象（比如曲率）的描述和定义更容易，同时最终会帮助我们构建不用过多考虑特殊情况和陷阱的高效明确的算法。微分几何的基本简化假设是我们想要去学习的被称为流形（manifold）的形状。 不精确的讲一下这个意思，至少在显微镜下，它们看起来和普通的欧式空间一样。比如，当你站在（球形）的地球表面上，很难告诉你并不是站在一个平坦的平面上。流形的假设是非常强有力的，因为它让我们将许多我们已知在平坦欧式空间中的操作（比如使用向量、微分和积分等）转移到更有趣的曲线空间。实际上有很多种使形状“看起来像欧式空间”的方法，致使微分几何有很多不同的分支（微分拓扑、共形几何、黎曼几何……）。现在，我们想聚焦在曲面完全基础的性质上，即在任意一个点周围你都可以找到一个小领域被称为拓扑盘（topological disk）。

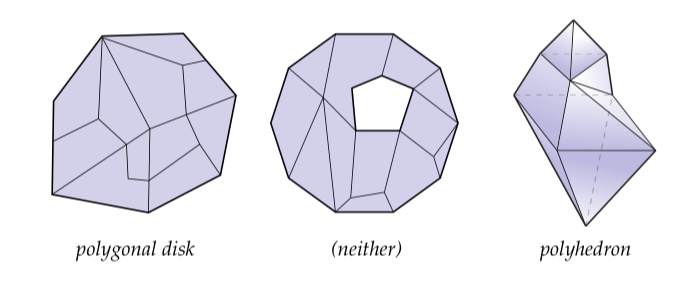
所谓拓扑盘，粗略来说，是指在不撕破、不穿孔且不粘合边的前提下通过形变一个平面中的单位盘可以得到的任一形状。包括旗帜、叶子和手套（半手指手套可能有点问题，因为穿孔了哈哈哈哈哈哈）都是盘形状的样例。一些不属于盘的形状包括圆圈（盘不包括其内部）、实心球、空心球、甜甜圈、指尖陀螺（fidget spinner）和茶壶。比如，对于上图我们有拓扑盘（左）、拓扑环（中）和将有限个多边形沿着它们的边粘合在一起的拓扑（球）结构。

在这一章中我们由定义一个抽象单纯复形开始，它将一个形状分解成简单的构件，比如边、三角形和四面体。任何一个抽象单纯复形都可以由一个关联矩阵（incidence matrices）编码，关联矩阵就是一个大的列表记录了哪些元素和哪些元素关联。虽然这种描述可以刻画一些相当复杂的形状，但是它通常比我们在离散微分几何中真正所需的更具有一般性（more general）。因此我们介绍一下半边网格（halfedge mesh），它是为二维曲面量身定制的，并且可以容易地使用一般的多边形（不仅仅是三角形）描述曲面。半边网格将作为这份笔记中绝大多数算法的基本数据结构。在这一章的结尾，我们将做一些测试，这些测试展现了组合曲面一些有意思的和有用的性质，并且可以通过写一些与组合曲面交互的代码对这些表示如何组合在一起获得一些直观感受。（这份翻译暂时没有翻译习题的计划）

抽象单纯复形

我们如何使用有限的信息编码曲面，使得将球与环区分开来是可能的？现在，让我们忘记形状或者几何（形状大小、厚度等），并且完全聚焦在连通性上：曲面的哪些部分和其它的相连，怎么连接的？

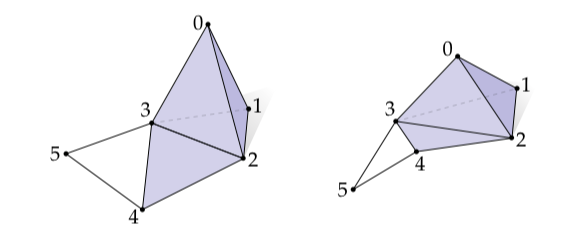
图1. 一个抽象单纯复形具体描述了顶点是怎么连接的，但是没有说它们在空间的哪个位置。比如，上面的两幅图都表示同一个单纯复形，由6个顶点、10条边、5个三角形和1个四面体。

有很多不同的方式描述一个离散曲面的连通性；一个方法是使用单纯复形，它实际上能编码比曲面复杂得多的对象。基本想法开始于顶点集合$V$，我们使用一系列整数来区分这些顶点：

$V = \{0, 1, 2, \dots, n\}$

我们同时也需要一些关于这些顶点如何连接的信息。单纯复形的想法是具体说明这些顶点中“右边邻接其它部分”的子集，被称为k-单纯形（k-simplices）。这个数字$k \in \mathbb{Z}_{>=0}$是一个非负整数，告诉我们这个集合内有多少元素：一个抽象的k-单纯形（k-simplex）是$(k+1)$个顶点的集合，我们将$k$称为这个单纯形的度。比如，这里有一个三角形或者2-单纯形：

$\{3,4,2\}$

这里还有一个1-单纯形:

$\{3,5\}$

从几何原理上来讲，我们可以将2-单纯形具体说明为三角形，1-单纯形为一条边，如图1左边所示；0-单纯形仅仅包含一个顶点。现在我们并不将顶点与具体的坐标联系起来，比如对于图1，右侧是另一个对这个单纯形的完美描写。因为这个原因所以我们将这些单纯形称作抽象的，它们不将一些具体的形状固定在空间中，而是仅仅（抽象地）告诉我们顶点是如何连接起来的。出于这个原因，我们可以在不必考虑这个东西在空间中看起来怎么样（3-单纯形、4-单纯形、5-单纯形……）的条件下走得尽可能高。同样地，我们（现在）不在乎这些顶点的顺序具体是什么样的：比如$\{2,3,4\}$和$\{3,2,4\}$表示同一个2-单纯形$\{3,4,2\}$。为了方便起见，我们将会经常使用对应的0-单纯形$\{i\} \in \mathcal{K}$确定任意一个顶点$i \in V$。

一个单纯形的任一（非空）子集都是另一个单纯形，我们称之为面（face）；一个严格子集被称为一个特有的（proper）面。比如，$\{2,3\}$是$\{3,4,2\}$的一个特有面，$\{2,3,4\}$是$\{3,4,2\}$的一个面但不是特有的一个。粗略来说，一个抽象单纯复形就是一个抽象单纯形的集合。然而，我们将在这个集合上放一个非常基本的条件，以此保证我们可以用一个自然的方式使用它，并且最终会帮助我们和平滑曲面联系起来。特别的，我们将会说单纯形的集合$\mathcal{K}$是一个单纯复形，在所有单纯形$\sigma \in \mathcal{K}$且每一个面$\sigma' \subseteq \sigma$也属于$\mathcal{K}$的条件下。比如，一系列三角形不能成为一个单纯复形；你必须同时包含它们的边和顶点。我们将通常假设一个单纯复形是有限的（比如，包含有限多个单纯形），虽然原则上你没有理由不能考虑一个无限的复形，比如整个欧式平面的三角网。

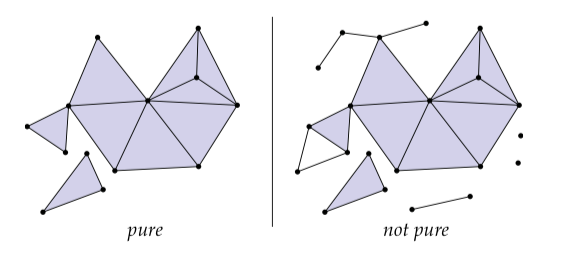
一个单纯复形$\mathcal{K}$的子复形（subcomplex）$\mathcal{K}'$是一个同样是单纯复形的子集。比如，一条单独的边并不是任一复形的子复形，但是带两个顶点的边是一个子复形。一个复形$\mathcal{K}$是一个纯k-单纯复形（pure k-simplicial complex），当每一个单纯形$\sigma'\in \mathcal{K}$都被包含在一些度为$k$的单纯形（可能是它自己）中。比如，一系列有顶点和边挂在上面或者独立漂浮在周围的三角形是非纯的：

最后，我们使用一个非常简单的（抽象的）对象结束：一个抽象单纯复形是整数的一个子集，在取子集的操作下是闭合的。这个诱导性的简单对象使得恰好编码任意曲面的拓扑都是可能的，不用担心多么复杂。为了做离散微分几何，我们最终将需要将一些类型的形状与一个单纯复形联系起来。但是现在已经有一些在纯组合设定下我们可以讨论的与曲面相关的有趣的东西。

单纯复形剖析：星、闭包和链环

当使用单纯复形时，能快速和简要地查阅到许多元素和区域是有帮助的。让我们开始于只考虑一个顶点$i \in V$。这个顶点的（单纯）星（star），记为$St(i)$，是满足$i \in \sigma$的所有单纯形$\sigma \in \mathcal{K}$的集合。考虑下面的例子：

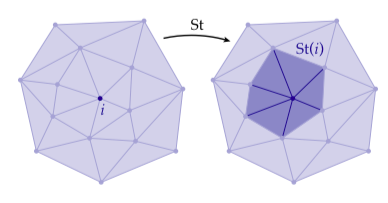
从这个图中，可以感觉到$St(i)$是$i$的某种“局部邻域”。然而，这个邻域它自己不是一个单纯复形，因为它没有包含“外面的”边。为了获得这样的一个复形，我们可以考虑$St(i)$的闭包（closure）$Cl$，它是$\mathcal{K}$中包含$St(i)$的最小子复形：

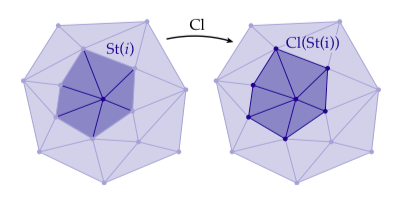
如果我们换个方向考虑，在获得星之前获得闭包呢？换句话说，我们首先考虑$\mathcal{K}$中包含$i$的最小子复形作为闭包$Cl(i)$。由于$\{i\}$没有特有的面，这个闭包就仅仅是这个顶点自己。如果我们继续获得这个星，我们会得到一个和上面第一次得到的同样的图，即$St(Cl(i)) = St(i)$：

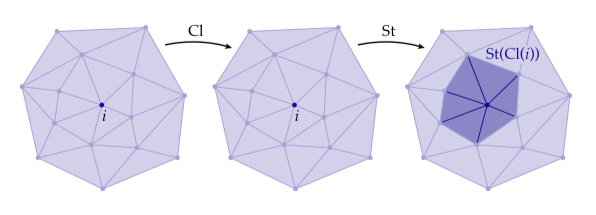
这两个集合仅有的区别是外壳边组成的环，这些边起初是不在我们的子复形中的。我们给这个集合一个特殊的名字：链环（link）$Lk(i) = Cl(St(i)) \setminus St(Cl(i))$ （其中$A \setminus B$表示集合差，即所以在A中且不在B中的元素）：

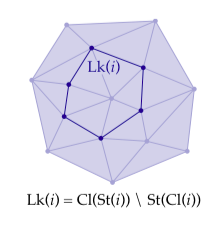
更一般的说，对于单纯复形$\mathcal{K}$中的任一子集$S$（不必是子复形），我们有如下定义：

• 星$St(S)$是$\mathcal{K}$中包含$S$中任一单纯形的所有单纯形集合
• 闭包$Cl(S)$是$\mathcal{K}$中包含$S$的最小（即元素最少）子复形
• 环$Lk(S)$等于$Cl(St(S)) \setminus St(Cl(S))$

另一个紧密相关的对象是纯k-子复形$\mathcal{K}' \subseteq \mathcal{K}$的边界（boundary）$\text{bd}(\mathcal{K}')$。边界是$\mathcal{K}'$中只属于一个单纯形特有面的所有单纯形所组成集合的闭包。这个定义自然地捕获到了你对集合“边界”可能的想法。比如：

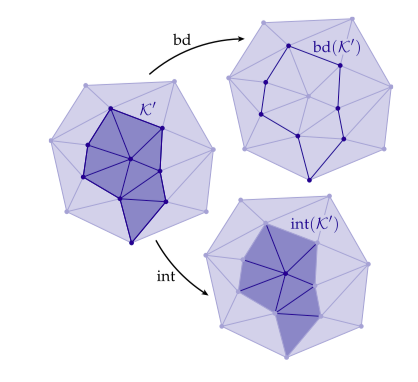
内部（interior）$\text{int} (\mathcal{K}') = \mathcal{K}' \setminus \text{bd}(\mathcal{K}')$是除了边界之外的所有东西（如上图所示）。

一般来讲，这些操作（星、闭包、链环、边界和内部）提供了一个自然的方式在任意维度中讨论和导航任意一种单纯复形。实际上，它们比我们仅仅需要讨论的简单组合曲面在合理程度上更一般。简单说一下，我们将介绍一个被称为半边网格（half edge mesh）的不同方法在组合曲面上导航，它在某些方面更“圆滑“并且在我们不考虑一般情况的时候更容易操作。但是为了这么做，我们首先需要定义我们真正需要用组合曲面表示什么——为了这么做，我们需要星、闭包和链环！

有向单纯复形

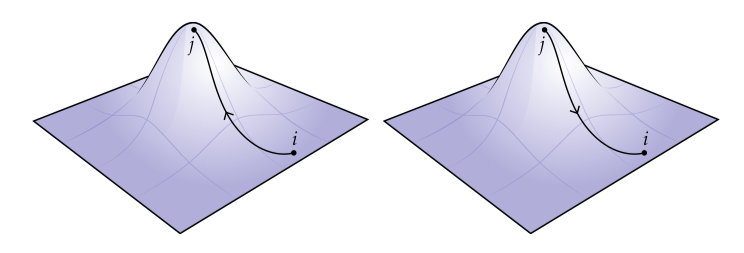
目前我们的假设是单纯形中顶点的顺序是无所谓的，并且使用集合来确定单纯形。比如，$\{i,j,k\}$是有顶点$i,j,k$的三角形，并且$\{j,i,k\}$或者$\{k,j,i\}$描述了同样一个三角形。但是在很多情况下，我们想要使用不同的方向区分单纯形，因为方向编码了关于我们正在测量和计算的量的一些信息。比如：山底到山顶的海拔变化和山顶到山底的海拔变化是相反的。

为了获取方向的概念，我们以使用有序元组替换无向集合开始。比如，如果$i,j \in V$是一条边的两个顶点，然后我们有两个不同顺序的元组$(i,j)$和$(j,i)$。第一个元组描述的是从$i$到$j$的有向边，然而第二个元组表示的是$j$到$i$。对于度更高的单纯形（三角形、四面体等），这个故事讲起来会更复杂一点。比如，考虑三个顶点$i,j,k \in V$构成的三角形。不仅仅只有一个有向集$\{i,j,k\}$，我们现在有六个可能的有序元组：

$\begin{matrix} (i,j,k) & (i,k,j) \\ (j,k,i) & (j,i,k) \\ (k,i,j) & (k,j,i) \end{matrix}$

这些元组的每一个都特定了围绕这个三角形的方法。比如，我们可以先到$i$，然后到$j$，然后到$k$。或者我们可以先到$j$，再到$i$，再到$k$。如果我们考虑这六种不同的可能，我们注意的是它们分为两个明显的种类：我们“顺时针”或者“逆时针”围绕这个三角形。这两种可能描述了对于我们的三角形来讲的两种可能的方向：

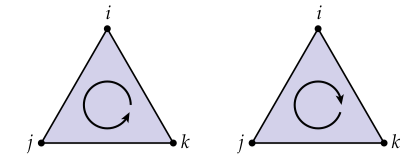
由于我们没有考虑起点，单纯形的一个方向实际上是有序元组的一个等价类（equivalence class）——这种情况下，上面元组的第一列全部是等价的（顺时针），第二列也是全部等价的（逆时针）。因此，为了确定一个有向三角形，我们将给出一个典型的三重索引，而不是单拿出一个特殊的元组出来。比如，我们将说：

$ijk \coloneqq \{(i,j,k), (j,k,i), (k,i,j)\}$

和

$ikj \coloneqq \{(i,k,j), (j,i,k), (k,j,i)\}$

希望这可以带来直观感受：使用圆括号写的元组描述了一个绕三角形的特殊路径；一个原始的三重索引表示具有等价方向的所有元组。从根本上来说我们总是会使用后者，因为它给了恰好足够的信息去知道我们正在讨论哪个有向单纯形：它的顶点和它的方向。

更一般地，对任意k-单纯形我们有两个可能的方向：顶点所有偶置换的集合，和顶点所以奇置换的集合（这块涉及到置换群）。比如，对于一个边我们只有$ij=\{(i,j)\}$和$ji=\{(j,i)\}$。对于一个三角形我们有上面已经给出的两个方向$ijk$和$jik$。对于一个四面体我们有$ijkl$和$jikl$。等等。仅仅只有0-单纯形是例外的，只有一种方法去写出顶点列表（即$i = \{i\}$）。一个0-单纯形因此仅有一个可能的方向。

如果两个有向单纯形有共同的顶点，那么我们就可以谈论它们的相对方向。比如，有向三角形$ijk$和$jil$有同样的方向（它们都是“顺时针”的），然而$ijk$和$ijl$是相对方向：

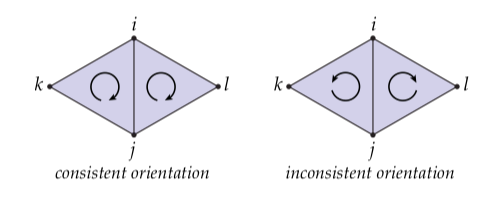
同样地，边$ij$与$ijk$有相同的顺时针方向，然而$ji$的方向是与之相对的。一般情况下，如果两个k-单纯形$\sigma_1$和$\sigma_2$有同样的$k-1$（-单纯形）顶点，那么它们有相同的方向当它们在这些共同顶点上的限制是相对方向的。对于任一有向单纯形$\sigma$，一个特有面$\sigma'$有相同的方向当$\sigma'$出现在$\sigma$的一些偶置换中。一个重要的特殊情况是0-和1-单纯形：一个有向边$ij$与$j$有同样的方向，但是与$i$有相对的方向；这个惯例刻画了$ij$是从$i$到$j$的事实。

一个（抽象）有向单纯复形是一个抽象单纯复形，其中每一个单纯形都分配了一个方向。即，我们开始于一个普通的单纯复形，并且简单的给每一个单纯形从两个方向中选择一个。这些方向上没有任何的条件：它们可以被随意分配。虽然（当可能时）通常方便地假设有公共(k-1)-面（单纯形）的k-单纯形有同样的方向（比如，一个平面三角网中的所有三角形都有顺时针方向）。

单形曲面

就像在这部分开始提到的一样，一个一般的单纯复形比我们需要学习的普通形状（帽子、脸、心脏，香蕉）更具有一般性，它们都可以用曲面完美刻画。相反的，使用抽象单形曲面（abstract simplicial surface）通常已经足够了。一个抽象单形曲面是一个纯单纯2-复形，其中每个顶点的链环是边的一个闭环，或者等价的，其中每个顶点的星是三角形构成的组合盘。实际上每个顶点有一个“盘状”的邻域刻画了拓扑曲面的基本思想；我们因此说这样的一个复形是流形。

不像一般的单纯复形，一个单形曲面不能有像多个三角形在同一个边处相邻这样的特性，或者多个顶点的“锥”在一个顶点处相邻。我们后面将会把这些配置成为非流形（nonmanifold）：

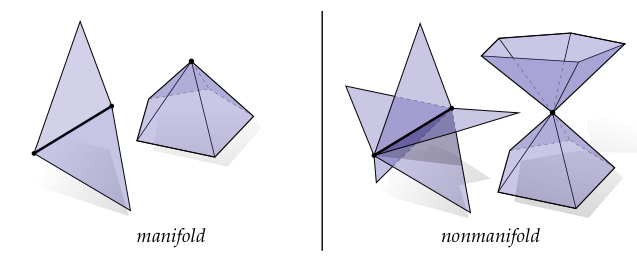
我们可以通过允许链环可以是一个简单的边的路径而不是一个闭环，使用边界扩展一点我们对单形曲面的定义：

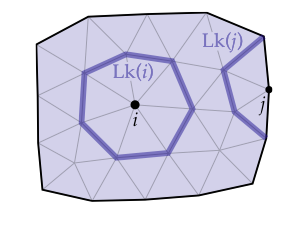
对于任一单形曲面$\mathcal{K}$，它的边界$\text{bd}(\mathcal{K})$将永远是（0个或多个）闭环的一个集合。

一个有向的单形曲面是一个抽象单形曲面，其中我们能给每一个三角形分配一个一致的方向，即其中任意两个有公共边的三角形给定相同的方向。我们后面将假设对于面可以是一致性方向的任一单形曲面有一致性的方向。一致性方向总是可以做到的吗？第一眼看这个问题的时候，它看起来很简单：从任意一个三角形开始，随意给它分配一个方向，现在“向外生长”，给每一个遇到的三角形分配一个一致的方向。这个问题在于，在一些时候，你可能在背后回环了并且发现没有任何一个办法可以给这个新的三角形分配一个一致性的方向，但是它和之前所有的方向都一致。考虑这个组合莫比乌斯带的例子：

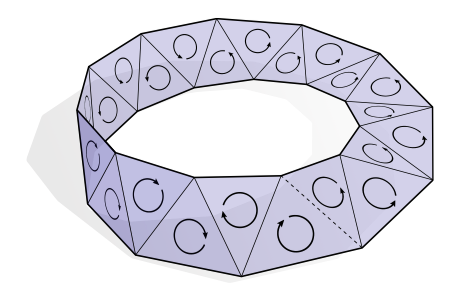
这种不可定向（unorientable）的曲面不会经常在自然界中出现——虽然它们值得被意识到它们是能存在的！

我们对于单形曲面的定义简单地扩展到高维：一个（组合或抽象）单形n-流形是一个纯单形n-复形，其中每个顶点的链环是一个单形(n-1)-球。一个单形n-球就是一个n-维球的（单形）三角网格

$\mathbf{S}^n \coloneqq \{ x \in \mathbb{R}^{n+1} : |x|=1 \}$

即n-维空间中到原点单位距离所有点的集合。比如，$\mathbf{S}^2$就是一个普通的单位球；$\mathbf{S}^1$是一个单位原；$\mathbf{S}^0$就只是一对点。一个单形曲面是一个单纯2-流形：每一个链环都是一个单形1-球，即边的一个闭环。一个单纯3-流形是一个四面体网格，其中每一个顶点都被球的一个三角网格围绕。等等。然而一个单纯1-流形怎么样呢？这可能意味着每个顶点的链环是一对点，因此单纯1-流形必须是闭环的集合（你认为为什么呢？）。

从此关于单形曲面我们还有大量更多的东西可以讨论，但是我们现在将着手开始这个事情。尤其是它足够让我们定义半边网格，这将是我们在单形（和更一般的，多面体）曲面导航的基本方式。

邻接矩阵

有一个很好的编码抽象单纯复形的方法是使用邻接矩阵，它将使得在单纯复形上的计算变得更加容易（通过线性代数的方式）。这些矩阵也和离散微分形式（discrete differential forms）联系非常紧密，这种形式给许多我们的几何算法提供了基础。

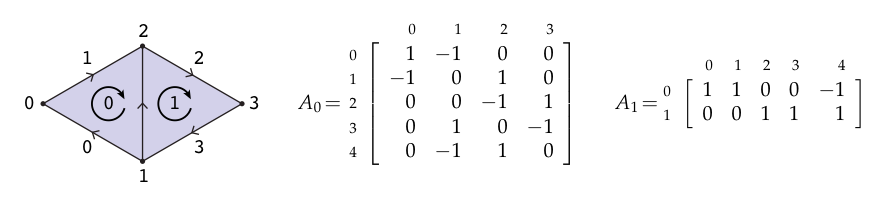
第一件必须要做的事情是给每一个度的单纯形都分配不同的索引。比如，我们有一个复形$\mathcal{K}$由顶点$V$、边$E$和三角形$F$构成，然后我们可能分配索引$0,\dots,|V|-1$给顶点，分配$0,\dots,|E|-1$给边，$0,\dots,|F|-1$给三角形。每一个顶点要分配给哪一个三角形不是很重要，只要对于每一个度的单纯形每个索引都只使用一次。比如，这有一个单纯2复形，我们标记了所有的顶点、边和面：

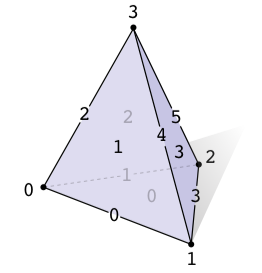
为了记录单纯形是怎么连接的，我们将储存一个矩阵$A_0$，它将说明哪条边包含了哪几个顶点，另一个矩阵$A_1$说明三角形包含哪些边，等等。我们将"1"放在矩阵$A_0$的$r$行$c$列中，表示第$r$个三角形中包含第$c$条边。等等。因此，邻接矩阵$A_k$的列数和k-单纯形的数量相同；行数是(k+1)-单纯形的数量。这个例子中，我们的矩阵看起来是这样：

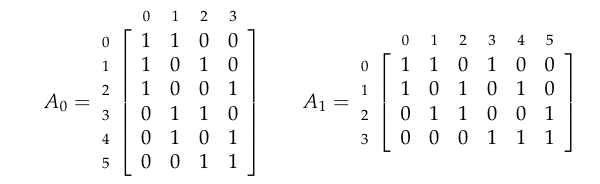
这里有一个需要注意的重要事项——对于连接数很少的特别大的复形——大多数元素都将是0。在实际使用中，因此使用稀疏矩阵是完全必要的，即一种有效的仅仅只储存非零元素位置和值的数据结构。稀疏矩阵数据结构的设计是一个完全取决于它自身的有趣的问题，但是在概念上你可以想象就是简单的元组$(r,c,x)$链表，其中$r,c \in \mathbb{N}$表示非零元素的行和列索引并且$x \in \mathbb{R}$给出它的值。

如果我们有一个有向单纯复形，我们可以构建一个带符号的邻接矩阵，它在连接性上加入了相关方向。仅有的改变是每一个非零元素的符号依赖于两个相关单纯形的相对方向：当有相同方向时为$+1$；方向相反时为$-1$。比如，这里有一个关于一对共享一条边方向一致的三角形的符号邻接矩阵：

半边网格

就像我们上面讨论的那样，我们在自然界中遇到的很多形状都可以用流形或可定向曲面很好的刻画。我们的第三种且是最后一种曲面编码方法，半边网格，利用了这种曲面所具有的特殊结构的优势。从某些方面来讲，这种编码方式相对于邻接矩阵表示来讲具有更低的一般性：我们不能刻画悬挂在三角网格上的边，或者莫比乌斯带状的曲面，或者更高维度的形状（比如体积而不是曲面）。另一方面，它能让我们使用一般的多边形描述组合曲面而不是只用三角形，在一些确定的重要情况中甚至允许我们相比于使用任意单纯复形使用更少的三角形（或多边形）。（正式的，一个半边网格允许我们将一个曲面编码成2维CW复形，具体参看参考文献）。

从我们在单纯曲面中的讨论我们可以注意到一些关于任意有向单纯曲面（我们现在假设没有边界）的东西：

• 每一条边都被两个多边形包含
• 围绕一个顶点的边可以赋予一个首尾循环的顺序

事实上，当曲面是由n条边的多边形组成而不仅仅是3条边的三角形时，声明依然成立：

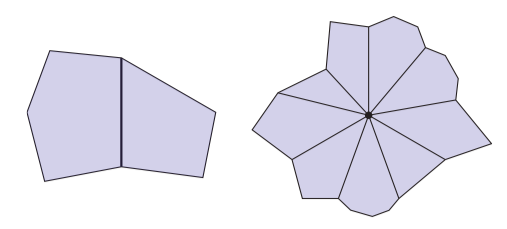
半边网格利用了特殊结构的优势来给曲面提供一个专门的精致的描述。基本想法是对于每一个无向边，$i,j$中间的$\{i,j\}$，在我们指定的上下文中我们有两个有向边$ij \neq ji$被称为半边。我们将使用$H$表示所有半边的集合；注意对于一个没有边界的曲面$|H| = 2|E|$，即我们的半边数是边的两倍。我们可以使用半边是如何连接的信息去描述一个有向的单纯曲面。特别的，我们有两个关键函数：twin和next。这个twin函数是映射$\eta : H \rightarrow H$：

$\eta(ij) = ji$

即它仅仅获得与这个半边有相同顶点但是方向相反的另一个半边。这个next函数是映射$\rho : H \rightarrow H$：

$\rho(ij) = jk , \forall ijk \in \mathcal{K}$

即从有向三角形$ijk$的半边得到围绕这个三角形的下一个半边。当我们拥有曲面的一些其它描述时（比如一个有向单纯复形或者一对邻接矩阵），这些映射合理地直接计算。

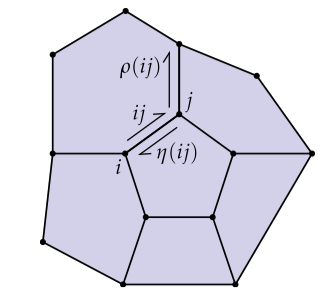
换个角度，我们可以只使用$\rho$和$\eta$这两个映射而不使用其它任何东西容易地得到这个多边形网格的点、边和面。比如，为了得到面我们可以开始于一些半边$i_1i_2$，并且使用映射$\rho$得到下一个半边$i_2i_3 = \rho(i_1i_2)$，然后再下个半边$i_3i_4 = \rho(i_2i_3)$，然后再下一个，直到我们最后返回到$i_1i_2$。换句话说，网格的面使用“下一个”映射$\rho$的轨道（orbits）来描述。那么“双胞胎”映射$\eta$的轨道能给我们带来什么呢？开始于$ij$我们得到$ji = \eta(ij)$，然后$ij = \eta(ji)$。因此，$\eta$的轨道描述了边。为了得到顶点，我们要变为使用映射$\rho \circ \eta$，即首先我们获得twin半边，然后获得next半边，然后twin，然后next，…，直到我们回到开始的地方。总结一下：

• 面是$\rho$的轨道
• 边是$\eta$的轨道
• 顶点是$\rho \circ \eta$的轨道

实际上，任何一对满足一些非常基本性质的映射$\rho,\eta$都能描述一个有效的组合曲面。所有我们需要的是（1）集合$H$元素个数是偶数，（2）$\rho$和$\eta$都是这个集合的排列，（3）$\eta$是没有固定点的对合（involution），即对于所有的$ij \in H$都有$\eta(\eta(ij)) = ij$，并且对于任一$ij \in H$都有$\eta(ij) \neq ij$。这最后一个条件可以这么通俗理解：它是说你双胞胎的双胞胎是你自己，但是你自己不是你自己的双胞胎。（如果这个条件对于真实的生物上的双胞胎不是成立的，那会是很严肃的问题！）只要$\rho$和$\eta$满足这些基本条件，我们就可以得到它们的轨迹并且找到一个组合曲面。

实际上，如果我们用特殊的方法标记我们的半边，我们甚至不用真正去担心$\eta$。特别的，假设我们分配0和1给第一对半边，2和3给第二对半边，等等。那么$\eta$就有了一个非常简单的描述：任何一个偶数$h$的twin是$h+1$，任何一个奇数$h$的twin是$h-1$。这个曲面的组合将完全由排列$\rho$定义。总的来说，每一个偶数排列都描述了一个组合曲面！这非常的怪异。但是确是真的！当下一次你遇到一个排列的时候可以思考下这个东西。

注意到甚至对于由三角形组成的曲面，半边网格可以描述这个曲面但是单纯复形不行。考虑如下的样例：

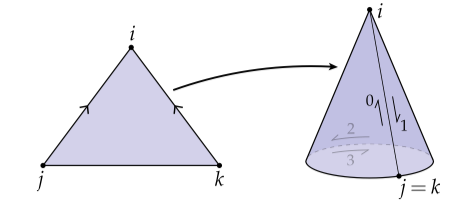
这里我们通过将三角形$ijk$的两条边粘合在一起得到了一个锥。如果我们使用一个圆盘补上这个锥的底部，那么我们会得到四个半边：三个半边$h_0,h_1,h_2$围绕这个三角形，还有一个半边$h_3$是围绕这个盘。这个next映射给定为$\rho(h_0) = h_1, \rho(h_1) = h_2, \rho(h_2) = (h_0)$和$\rho(h_3) = h_3$，即我们有一个绕三角形的闭环和一个绕圆盘的闭环。这个twin映射使用关系$\eta(h_0) = h_1$和$\eta(h_2) = h_3$，即两个两个三角形半边粘合在一起，和剩下的三角形半边与绕盘半边粘合在一起。没有办法使用单纯复形（有向的或其它）去描述它：一个单纯复形仅仅允许我们确定一个三角形$ijk$；我们无法去确定边是如何粘合在一起的。同样的，包括这个盘也完全超出了问题界限：它甚至不是一个普通的多边形，更像是一个“unigon”（这个词不会翻，给了一个查到的链接作为参考）。这里有另一个有趣的例子：

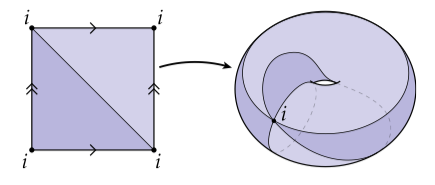
此时我们有了由两个不同的三角形组成的环面，但是只有一个顶点。（你能写出对应的映射$\eta$和$\rho$吗？）显然没有办法使用单纯复形去描述它：因为一个原因，“集合”$\{i,i,i\}$不是一个集合：它没有三个能区分的顶点。甚至就算我们允许重复（即多重集合（multi-sets）），我们也没有办法在单纯复形中区分两个不同的三角形"$iii$“和”$iii$"，并且没有办法解释这些三角形是如何粘在一起的。半边网格处理这种情况就很容易，并允许我们使用更少的元素去描述有趣的空间。相对而言，使用单纯复形描述环面至少需要7个顶点，21条边和14个三角形：

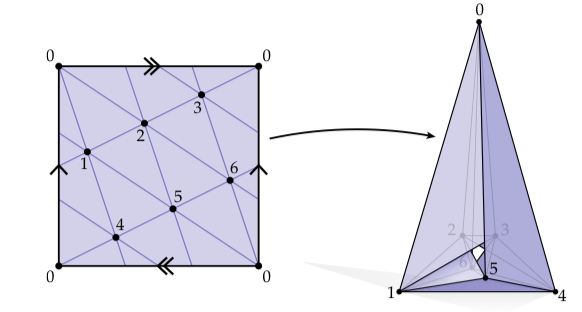
这里我们使用两种方式画下了这个三角网格：左边，我们将它画到平面上并且想象它的左/右和上/下粘合在一起。足够令人感到惊奇的是，同样的三角网格可以使用在$\mathbb{R}$中的直线和平坦且不相交的三角形画出来，就像右边展示的一样——这个东西被称为Cs´asz´ar多边形。不管是哪种情况，相对于我们使用半边网格得到的环面的两个三角形的分解它都更加复杂。

在使用水平上，半边描述将给我们在这份笔记中实现的算法提供基本数据结构。通过得到“下一个”和“双胞胎”半边，你可以容易地获得你内心渴望的任何网格。虽然这里有最后一个问题：我们如何处理带边界的曲面（比如盘或者圆环）？似乎违反我们基本公理中的一个，每一条边都恰好被两个多边形包含。这个简单的答案是：仅仅将每个边界部分看作一个带有很多边的多边形。换句话说，把你带边界的曲面转换为不带边界的曲面，通过简单的“补洞”（用一些方法制造一些额外的多边形）。这样你就有了一个不带边界的曲面，你就可以像往常一样处理它了。