DDG（离散微分几何）：对微分几何快速粗暴的一个介绍

翻译自 DISCRETE DIFFERENTIAL GEOMETRY: AN APPLIED INTRODUCTION 第三章 A Quick and Dirty Introduction to Differential Geometry。如果有翻译错误或者不当的地方希望能指出，谢谢～

曲面的几何

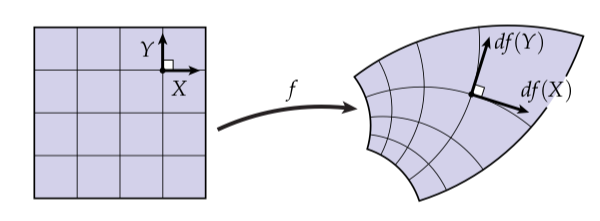
有许多方法考虑平滑曲面的几何（比如，地图集），但是这里有一张图很贴合我们在离散设定下操作曲面的方式。考虑一个小布块悬浮在空中，像下面描绘的一样。它的几何可以通过从欧式平面$\mathbb{R}^2$中的一个区域$M$到$\mathbb{R}^3$子集$f(M)$的映射$f:M \rightarrow \mathbb{R}^3$表示：

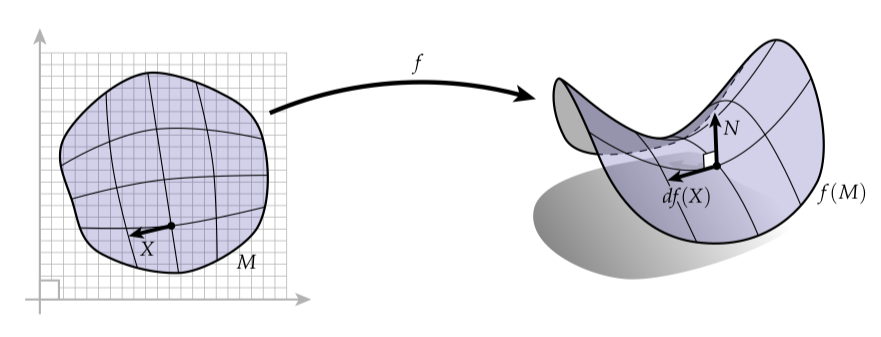
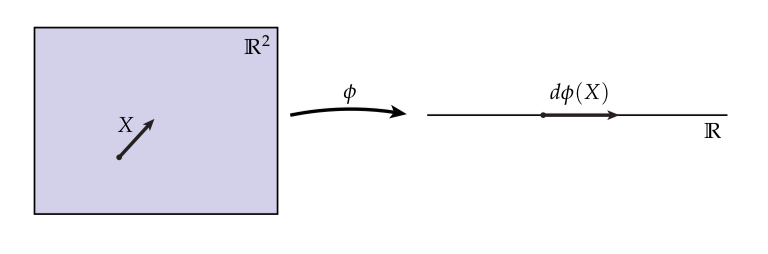
这样一个映射的微分（differential），记为$df$，告诉我们如何将平面上的一个向量$X$映射到曲面上对应的向量$df(X)$。粗略来讲，想象$M$是一个橡胶片，并且$X$是画在$M$上的一条小黑色线段。我们将$M$拉伸和形变为$f(M)$，这个线段$X$同样会被拉伸和形变为另一个线段，我们称之为$df(X)$。稍后我们讨论如何在坐标系中明确表示$df(X)$和其它的一些内容，但是重要的是意识到关于微分除了你刚刚看到的这张图基本上没有更深层次的东西需要知道——微分简单地告诉你当你从一个空间到另一个空间的时候是如何拉长或者“向前推”向量的。比如，被$f$向前推后的正切向量$X$的长度可以表示为

$\sqrt{df(X) \cdot df(X)}$

其中 $\cdot$ 是$\mathbb{R}^3$上的标准内积（点乘或者数乘）。注意到这个长度和我们刚刚开始的向量长度一般来讲是不同的。为了行文清晰，我们使用角括号表示平面中的内积，即原始向量的长度应该是$\sqrt{\langle X, X \rangle}$。更一般的，我们可以测量两个正切向量$df(X)$和$df(\Upsilon)$之间的内积：

$\mathsf{g}(X, \Upsilon) = df(X) \cdot df(\Upsilon)$

映射$\mathsf{g}$被称为曲面的度量（metric），或者更专业一点，由$f$引导的度量。注意到全文中，我们将使用$df(X)$交换地表示单个向量的变动（pushforward，应该可以理解成拉伸和形变）与整个向量场，即$M$中每一个点的向量。在大多数表示中我们将考虑这种区别不产生大的歧义，但是值得我们注意一下。全文中我们将使用$TM$表示$M$的正切束（tangent bundle），即所有正切向量的集合。

现在我们谈到了正切向量，即沿着曲面平躺的向量。我们同样对与曲面正交的向量感兴趣。尤其是，我们说向量$u \in \mathbb{R}^3$是曲面在点$p$处点法线，当

$df(X) \cdot u = 0$

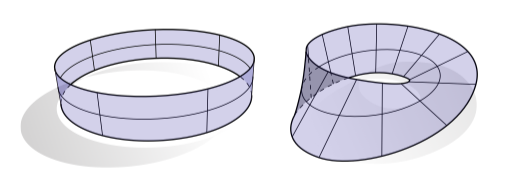
对所有$p$处的正切向量$X$。为了方便，我们通常给出唯一一个特殊的法向量$N$，被称为单位法线，它的长度为1。当然，在任何一个给定点处都有两个不同的单位法向量：$-N$和$+N$。我们应该用哪一个呢？如果我们可以为$N$选取一个一致的方向，那么我们称$M$是可定向的。比如，左边的环带是可定向的，但是右边的莫比乌斯带就不是：

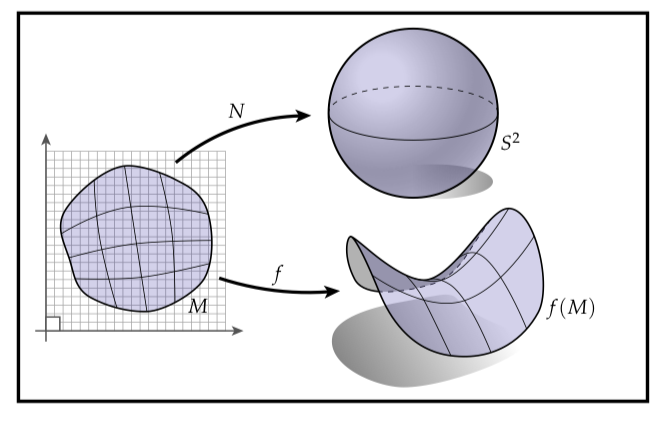
对于可定向曲面，我们可以把$N$看作连续映射$N:M \rightarrow \mathcal{S}^2$（被称为高斯映射（Gauss map）），它将每个点和它对应的单位法线联系起来，将每个点视为单位球$\mathcal{S}^2$上的点。实际上，如果我们将$\mathcal{S}^2$看作是$\mathbb{R}^3$的子集（所有到原点单位距离点的集合），那么我们可以对$N$做所有我们在映射$f$上做的事情。实际上，微分$dN$（被称为 Weingarten 映射）告诉我们当我们从一个点到另一个点的时候法线方向的变化。比如，我们可以看着沿着由$dN(X)$给出的特定正切方向$X$的法线变化——当我们谈论曲面曲率的时候这个理解会变得非常有用。综上我们用这个图来结尾，它表达了关于曲面集合最基础的想法：

共形坐标系

当在曲线上操作时，大家经常被介绍使用等距参数（比如，弧长或单位速度）的想法。这个想法通过假设当我们从当前域到$\mathbb{R}^3$的时候没有“伸长”发生使得明确的表达式更简单。一种表示这个规定的方法是

$|df(X)| = |X|$

即我们要求保证任何一个向量$X$的范数不变。

对于曲面，一个等距参数并不总是存在（甚至对于局部也是这样！）。绝大多数时候你简单的必须撑大一个东西。比如，你可能知道没有形变地将地球的曲面平铺在平面上是不可能的——这也就是为什么我们得到球形不同的古怪映射种类的原因。

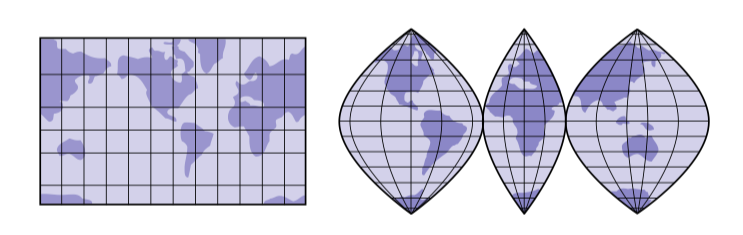
然而，有一个配置（就像对于曲线来说的弧长）当处理明确公式时能让生活更简单，它叫做共形坐标系（conformal coordinates）。十分简单的来说，一个映射$f$是共形的，当它保持两个向量之间的夹角不变时。更具体的来说，一个共形映射$f:\mathbb{R}^2 \supset M \rightarrow\mathbb{R}^3$对于所有的正切向量$X, \Upsilon$满足

$df(X) \cdot df(\Upsilon) = a\langle X, \Upsilon \rangle$

其中$a$是一个正定函数，$\langle \cdot , \cdot \rangle$是$\mathbb{R}^2$上的一般内积。实际上，对于一些实值函数$u$，函数$a$通常被$e^u$代替——这样的话就完全无需担心尺度是否为正了。注意向量仍然可以被拉长，但是曲面不会被剪断——比如，正交的向量永远保持正交：

关于共形映射的一个关键事实是它们总是存在，由单值化定理担保。简而言之，单值化定理说的是任意一个盘都可以被共形映射到平面上。使用如果我们考虑我们曲面$f(M)$上点任一一点$p$，我们知道我们总是能在$p$周围一些小的、盘状的领域找到一个共形参数化。正如单位速度的曲线一样，它通常足够去简单地知道一个共形参数化存在——我们不必明确去构造这个映射。并且，正如弧长参数化一样，我们必须保持关于这个域如何伸展的最少可能信息量的跟踪：仅仅是每个点处的一个数（对立的是，一个完整的雅可比矩阵）。

导数和正切向量

在实线上的导数

目前我们用了非常几何的方法来考虑微分：它告诉我们如何像从一个地方到另一个地方一样去伸长或者变动（push forward）正切向量。实际上，我们可以将几何观点应用到包括导数在内的非常多的情况中。比如，考虑一个很好的不是很古怪的在实线上的实值函数$\phi(x)$。我们使用一贯的方法，通过将$\phi$的值作为$x$轴上的高度绘制出来进行可视化：

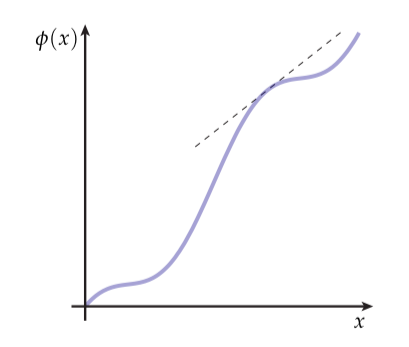
在这种情况下，导数$\phi'$可以解释为高度函数的斜率，就像上图中虚线表示的一样。或者说，我们可以想象$\phi$拉长了这个实线自身，由节点在这个图中分布的变化表示：

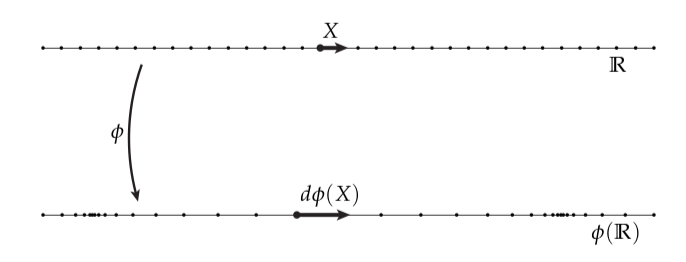
当导数大的时候，节点分布距离比较远；当导数小的时候，节点分布距离比较近。这个图告诉我们将$\phi$的导数写成指向正$x$轴方向的单位切向量$X$的变动项$d\phi(X)$：

$\phi' = d \phi (X)$

换句话说，$\phi$的导数就是当我们从一个$\mathbb{R}$的副本到另一个时的“伸长因子”。但是等一下——这个等式是否讲得通？这个等式的左边是一个标量，但是右边却是一个向量！当然，任何实线上的切向量都可以被表示成一个单独的值，量化它在正或负方向的大小。所以这个等式是讲得通的——只要我们理解我们是使用实数定义$\mathbb{R}$上的正切向量的。通常这种“类型校验”将帮助验证公式和表达是正确的，类似于你可能在物理等式中校验单位的方法。

这里又出现了一个问题：这个导数的解释和我们通常对高度函数项的解释有什么不一样吗？难道我们不也是在那种情况下拉长实线吗？是也不是——当然这个实线仍然拉长到另一个曲线。但是这个曲线现在是平面$\mathbb{R}^2$的子集——具体来说，它是曲线$\gamma = (x, \phi(x))$。所以其中一个原因是，这种情况下“类型校验”失败：$\phi'$是一个标量，但是$d\gamma(X)$是一个2维向量。但是最重要的是，由曲线表示的伸长量并不和我们通常的$\phi$导数符号对应——比如，当我们寻找$|d\gamma(X)|$的量时我们得到$\sqrt{1+(\phi')^2}$。（为什么这个声明是符号几何原理的？你会如何将$\phi'$写入$d\gamma(X)$项中？你能构造一个等式修复这个合适的符号吗？）

方向导数

目前为止的状态都很好：我们可以将$\mathbb{R}$上实值函数的导数考虑为（正向）单位切向量$X$的变动。但是当$\phi$定义在一些其它的域上时，比如平面$\mathbb{R}^2$，$d\phi(X)$表示什么呢？这个问题可能将你的思想“伸展”一点，但是如果你理解了这个例子你将很好地用你自己的方式理解正切向量项中的导数。让我们看看这个问题的几何——再一次，有两种我们描绘$\phi$的方式。通常的方式是在平面上画高度函数：

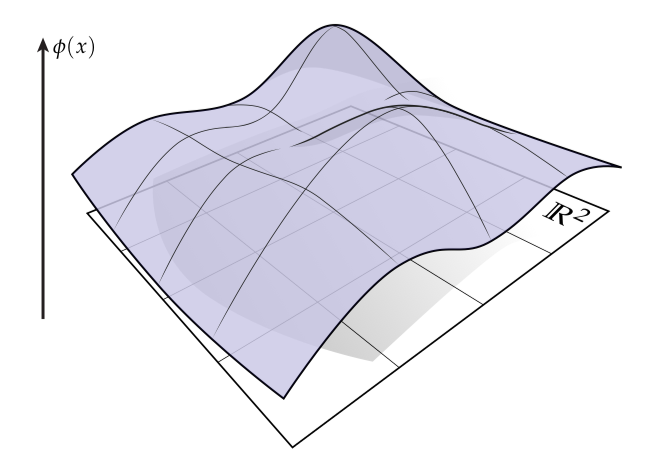
导数和坡的斜率相关，但是哪个方向呢？为了回答这个问题，我们将介绍方向导数（directional derivative）的想法——即我们选择一个向量$X$然后看我们在那个方向上山（或下山）有多快。然后再一次我们考虑一个转换后的图像：

由于$\phi$是一个从$\mathbb{R}^2$到$\mathbb{R}$的映射，我们可以想象它拿起了一个橡胶片然后将它拉成一个长的、细的、沿着实线的一维对象。因此当我们在原来的片上画上一个箭头$X$，然后这个“拉长后”的箭头$d\phi(X)$给我们$\phi$在沿着方向$X$上变化的比例，即方向导数。关于类型校验的情况呢？在此之前，将前面的东西回顾一下：$d\phi(X)$是$\mathbb{R}$上的正切向量，所以它可以通过单个实数表示。（在上面我们是怎么继续在高度函数上操作的？我们如何在这个情况下修复方向导数？）

顺便提一下，不要担心这个讨论看起来非常的不正式！当我们开始讨论外积分时，我们将看到一个对于这些想法更明确的、代数的探讨。现在重要的事情是对导数建立一些几何直觉。具体来说：从一个空间映射到另一个空间可以被看作几种弯曲、扭转和伸展（或者可能的撕裂！）；导数可以被理解为一个项，它按照这个方法发生在小箭头上。

曲线的几何

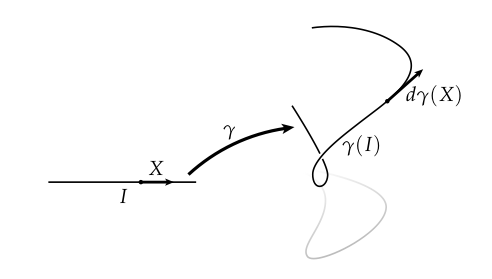
我们看到的曲面的图是一个关于理解任意维度形状的好方法。比如，我们可以将一个一维的曲线考虑为从实线区间$I = [0, T] \subset \mathbb{R}$到$\mathbb{R}^3$的映射$\gamma : I \rightarrow \mathbb{R}^3$，这个微分$d\gamma$再一次告诉我们正切向量如何通过$\gamma$伸展，并且再一次引入了正切向量$X$的长度为

$|d\gamma(X)| = \sqrt{d\gamma(X) \cdot d\gamma(X)}$

如果$\gamma$保长的话在曲线上操作将更容易，即如果对任意正切向量$X$有

$|d\gamma(X)| = |X|$

这种参数化有许多不同的名字（“单位速度”，“弧长”，“等距”），但是这个想法简单到我们从$\mathbb{R}$到$\mathbb{R}^3$时曲线没有伸展——将$\gamma$考虑为一个完全松弛的橡胶带。单位速度的观点对于我们没有基本域$I$的符号时的离散设置通常是合适的一个——从最开始，这个曲线就作为$\mathbb{R}^3$的子集给到我们并且我们能做的所有事情就是假设它在那里保持一个松弛的状态。

曲线的曲率

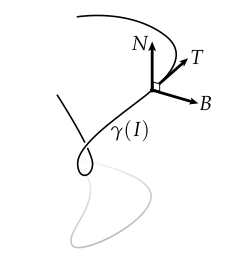
假设我们有一个单位速度的曲线$\gamma$和一个在区间$I$上的正向单位向量$X$。那么

$T = d\gamma(X)$

是$\mathbb{R}^3$中与曲线相切的单位向量。将这个想法向前推进一步，我们可以看到当我们沿着$\gamma$移动时切向的变化。由于$T$可能按照任何比例变化（也可能完全不变！），我们将这个变化分离为两个部分：一个被成为主法线（principal normal）的单位向量$N$表示变化的方向，和一个被成为曲率（curvature）的标量$\kappa \in \mathbb{R}$表示变化的程度：

$dT(X) = - \kappa N$

一个事情需要意识到，那就是$T$和$N$总是正交的。为什么？因为当$T$中的变化平行于$T$时，那么它将不再有单位长度！（这个观点是在处理单位向量场的任何时候都需要牢记在心的一个很好的观点。）按照习惯，我们选择$N$为指向曲线“左侧”的法线，即，如果在任一点处我们考虑一个由切向量和法向量张成的平面，$N$是从$T$往逆时针方向转四分之一得到的。此时也会带来第三个被称为副法线（binormal）的向量$B = T \times N$，我们得到一个被称为Frenet框架（Frenet frame）的非常自然的正交坐标系框架。

当我们沿着曲线运动时这个框架如何变化？答案由FrenetSerret公式（FrenetSerret formula）给出：

$\underbrace{\begin{bmatrix} T' \\ N' \\ B' \end{bmatrix}} _{Q' \in \mathbb{R}^3}= \underbrace{ \begin{bmatrix} 0 & -\kappa & 0 \\ \kappa & 0 & -\tau \\ 0 & \tau & 0 \end{bmatrix} }_{A \in \mathbb{R}^{3 \times 3}} \underbrace{ \begin{bmatrix} T \\ N \\ B \end{bmatrix} }_{Q \in \mathbb{R}^3}$

这里，$T$、$N$和$B$都被解释为行向量，带上标的表示当我们在单位速度下沿着曲线运动的量下的变化。比如，$T' = dT(X)$，当$X$是$I$上的正向单位向量。量$\tau$被称为扭转（torsion），描述法线和副法线围绕曲线缠绕（twist）的方式。

这个公式一个简洁的证明由Cartan给出。首先，由于向量$T$、$N$和$B$是互相正交的，我们可以非常简单的验证$QQ^T = I$，即$Q$为正交矩阵。此时将这个关系微分，这个单位矩阵会消失并且会剩下$Q'Q^T = -(Q'Q^T)^T$，即矩阵$Q'Q^T$是反对称矩阵（skew-symmetric）。但是由于$A = Q'Q^T$，$A$必须也是反对称的。反对称要求$A$的主对角元素必须为0（为什么？），并且我们早就从我们对$\kappa$和$N$的定义知道了顶行（因此知道了左列）长什么样。剩下的值$A_{23} = -A_(32)$没有被任何方式约束，所以我们简单地给它一个名字：$\tau \in \mathbb{R}$。

我们如何看待这个证明？一方面它很容易验证；另一方面，它提供了一点简单的几何理解。比如，为什么$N$同时在$T$和$B$的方向上变化，但是$B$只在$N$的方向上变化？你能想出更多的几何观点嘛？

可视化曲线

圆$\mathcal{S}$曲率是什么？当$\mathcal{S}$有半径$r$时，在单位速度下需要花费$2 \pi r$的时间去绕这个圆一圈。在这段时间中，切线方向转了$2 \pi$的角度。当然，由于$T$有单位长度，$T$上瞬间的变化仅仅通过角度的瞬间变化描述。所以我们最终得到（第三个等号是总变化/时间）

$\kappa = |\kappa N| = |dT(X)| = 2 \pi /2 \pi r = 1 / r$

换句话说，圆的曲率简单地就是半径的倒数。这个现实可以得到一些直观的感受：如果我们看到一个圆变得越来越大，它最终就会看起来像一个曲率为0的直线：\lim_{r\rightarrow \infin} 1/r = 0。类似的，如果我们看到一个圆越来越小，它最后看起来就会像一个有无穷曲率的点：\lim_{r\rightarrow 0} 1/r = \infin。

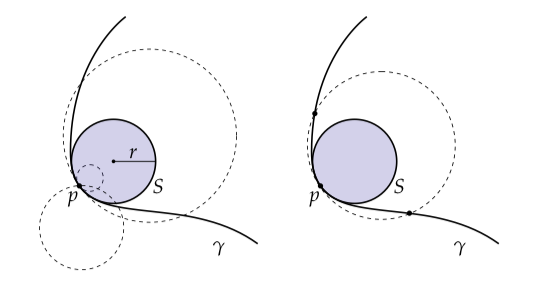
现在考虑一个平面中的平滑曲线$\gamma$。在任意一点$p \in \gamma$处都有一个被成为密切圆（osculating circle）的圆$\mathcal{S}$最好地拟合了$\gamma$，意味着它有同样的切向$T$和曲率向量$\kappa N$。换句话说，这个圆和这个曲线“到第二阶”一致。（这个短语“到第n阶一致”只是前n阶导数相等说法的速记。）我们如何知道这样的圆存在呢？简单：我们总是可以通过设置$r = 1/ \kappa$估计曲率构造一个圆；此外每个圆在方向$T$上有同样的切点。或者说，我们可以考虑一个圆，它穿过点$p$和其它的两个点：一个从左边靠近，一个从右边靠近。因此这三个点同时在$\gamma$和$\mathcal{S}$上，一阶和二阶导将在极限上相等（考虑这些点可以被用来获得$T$和$\kappa N$一致的有限微分估计）。

这个密切圆的半径和中心通常被分别称为曲率半径（radius of curvature）和曲率中心（center of curvature）。我们可以通过考虑密切面（osculating plane）$T \times N$对任意$\mathbb{R}^3$中的曲线讲述同样的内容，因为这个平面同时包含了正切向量和曲率向量。

对于曲线，我们用正切向量或者（主）法向量的变化项表示曲率不会造成什么不同，因为这两个向量于密切平面中在四分之一圈的旋转意义下等价。然而，对于曲面来说，它通常将曲率考虑为法向量的变化更合理，因为我们通常没有可以在上面操作的明确可以区分出的正切向量。

曲面的曲率

让我们更深入地来了解一下曲面的曲率。这个词“curvature”真正地对应了，对于某个东西被弯曲时，我们对它表示什么意思的日常理解：蛋壳、甜甜圈和某种意大利面食（这个真的不知道怎么翻译，cavatappi pasta）有大量的弯曲；地板、天花板和硬纸板箱就不是。但是对于一些看起来像啤酒瓶的东西呢？沿着其中一个方向这个瓶子快速地在绕着一个圆弯曲；沿着另一个方向它是完全平坦的并且沿着一条直线移动：

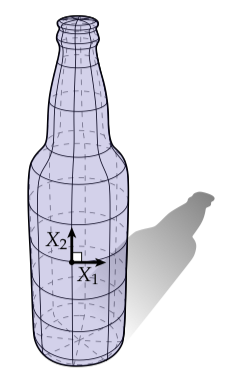
这个看待曲率的方式——包含在曲面中的曲线项——是通常我们看待曲率的方式。特别的，让$df(X)$是曲面上某个特定点处的单位切向，并且考虑同时包含$df(X)$和对应的法线$N$的平面。这个平面与曲面交于一条曲线，那么这条曲线的曲率$\kappa _n$被称为$X$方向上的法线曲率（normal curvature）：

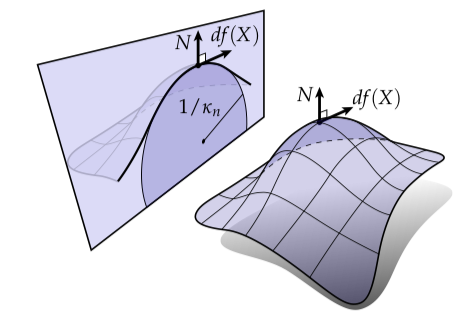
还记得Frenet-Serret公式吗？它告诉我们沿着曲线时法线的变化为$dN = \kappa T - \tau B$。我们因此能通过抽出$dN$无关的部分得到沿着$X$的法线曲率：

$\kappa_n(X) = \frac{df(X) \cdot dN(X)}{|df(X)|^2}$

这个分母中的因子$|df(X)|^2$简单地归一化了任何当我们从域$M$到$\mathbb{R}$中遇到的“伸长”。注意到法线曲率是带符号的，意味着曲面可以朝向法线方向弯曲或者反方向弯曲。

主曲率、平均曲率和高斯曲率

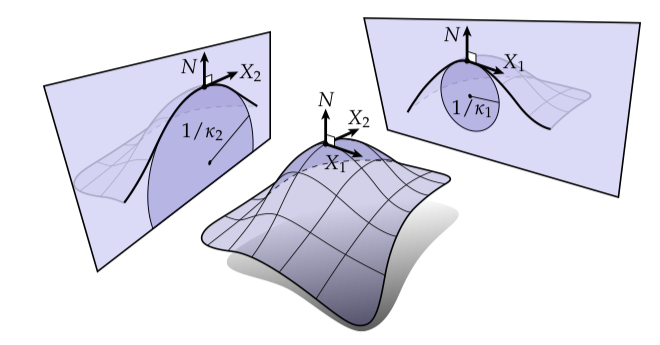
在任一给定点处我们可以问：沿着哪个方向这个曲面弯曲得最厉害？沿着我们找到的最大和最小法线曲率$\kappa_1$和$\kappa_2$的单位向量$X_1$和$X_2$被称为主方向（principal directions）；曲率$\kappa_i$被称为主曲率（principal curvatures）。比如，上面的啤酒瓶可能在标记的点处有主曲率$k_1 = 1$， $k_2 = 0$。

我们同时也使用形状算子（shape operator）项来讨论主曲率，它是一个单射$\mathcal{S}:TM \rightarrow TM$，对于所有的正切向量$X$满足

$df(SX) = dN(X)$

形状算子$\mathcal{S}$和 Weingarten 映射$dN$本质上表达的是同一个想法：它们都告诉我们沿着方向$X$移动时法线是如何变化的。唯一的不同是$\mathcal{S}$ 特指$M$上正切向量项的变化，而$dN$告诉我们的是$\mathbb{R}^3$中正切向量的变化。这个区别没有上面特定含义因此很多作者并不提及它，并且假设$M$上的正切向量和对应$\mathbb{R}^3$中的正切向量是等价的。然而，我们选择更小心一点，因此我们可以更明确的描述各种浸入（immersion）$f$上的依赖——这个依赖当你恰好想计算某些东西的时候变得尤其重要！（顺便，为什么我们总是可以使用正切向量项解释$N$的变化？那是因为$N$是单位法线，因此它不可能在法向上伸缩。）

一个关于主方向和主曲率的重要现实是它们（分别）对应形状算子的特指值和特征向量：

$\mathcal{S}X_i = \kappa_i X_i$

此外，主方向在引导度量的意义上是正交的：$\mathsf{g}(X_1, X_2) = df(X_1) \cdot df(X_2) = 0$。因此主曲率告诉了我们关于某点处法线曲率的所有事情，因此我们可以使用主方向$X_1$和$X_2$的线性组合表示任何一个正切向量$\Upsilon$。特别的，当$\Upsilon$是一个从$X_1$转了角度$\theta$的单位向量偏移，那么它对应的法线曲率为

$\kappa_n(\Upsilon) = \kappa_1 \cos^2\theta + \kappa_2 \sin^2\theta$

你应该能够使用上面的关系简单地验证。然而，通常来说直接使用主曲率是相当不方便的——尤其在离散情况下。

另一方面，两个紧密相关的量——被称为平均曲率（mean curvature）和高斯曲率（Gaussian curvature）将一次又一次出现（并且在离散情况中有一些特别好的解释）。平均曲率$H$是主曲率的算术平均值：

$H = \frac{\kappa_1 + \kappa_2}{2}$

高斯曲率是几何平均（的平方）：

$K = \kappa_1 \kappa_2$

那么$H$和$K$的值分别表示关于曲面形状的什么东西呢？可能绝大多数基本解释是高斯曲率类似逻辑“与”（是同时沿着两个方向的曲率吗？）而平均曲率更类似逻辑“或”（沿着至少一个方向的曲率吗？）当然，在这里你必须小心一点因为在$\kappa_1 = - \kappa_2$时你也会得到0平均曲率。

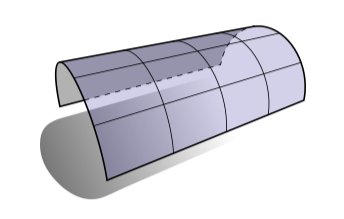
看一些0平均曲率和高斯曲率的图片同样是有帮助的。0曲率曲面在数学上已经被研究得很透彻了，因此它们有特殊的名字。0高斯曲率的曲面被成为可扩展曲面（developable surfaces），因为它们可以被“扩展”或者在没有拉伸或撕裂的情况下被平铺到平面上。比如，圆柱体的任意一片是可扩展的，因为主曲率中的一个是0:

0平均曲率的曲面被称为最小曲面（minimal surfaces），因为（就像我们稍后将看到的）它们最小化曲面空间（在确定的约束下）。最小曲面趋向鞍状，因为主曲率有相同的大小但是符号相反：

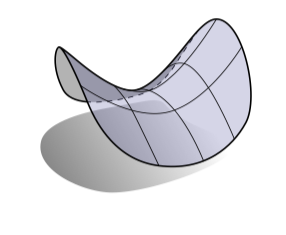
同时马鞍也是一个有负高斯曲率的很好的曲面例子。有正高斯曲率的曲面长什么样？半球是一个例子：

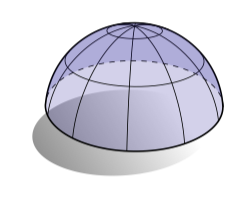
注意到这个情况下$\kappa_1 = \kappa_2$并且因此主方向并不是唯一定义的——沿着任何方向$X$都能实现最大（或者最小）曲率。曲面上任何一个这样的点被成为脐点（umbilic point）。有很多有趣的理论和关系涉及到曲率，但是这些是基本的事实：曲面的曲率可以由主曲面完整地描述，主曲率是最大和最小的法线曲率。高斯和平均曲率是两个主曲率的简单平均，但是（像我们将要看到的）在实际情况中通常更容易得到。

基本型

由于历史原因，我们应该提到两个对象：第一基本型（first fundamental form）$I$和第二基本型（second fundamental form）$II$。我并不确定这两个形式到底基本在哪里，因为它们除了将度量$\mathsf{g}$和形状算子$\mathcal{S}$组合在一起之外什么也没有表示，他们自己是两个真正基本对象的简单函数：浸入$f$和高斯映射$N$。实际上，第一基本型就仅仅是引导度量，即

$I(X, \Upsilon) \coloneqq \mathsf{g}(X, \Upsilon)$

第二基本型看起来十分像我们已有的法线曲面的公式：

$II(X,\Upsilon) \coloneqq -\mathsf{g}(\mathcal{S}X, \Upsilon) = -dN(X) \cdot df(\Upsilon)$

最重要的事情是意识到$I$和$II$并没有引入任何新的几何想法——仅仅对于我们已经看到的东西是换了一种写法。

坐标系中的几何

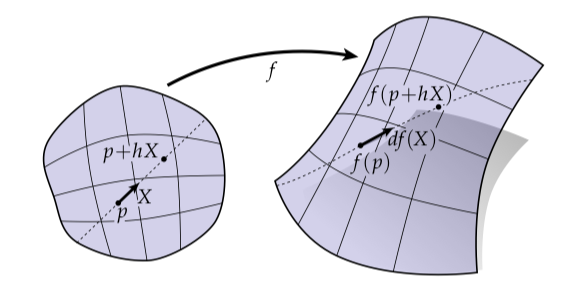
目前我们已经对于我们一直操作的几何对象给出了相当抽象的描述。比如，我们说过一个浸入$f:M \rightarrow \mathbb{R}^3$的微分$df$告诉我们当从域$M \subset \mathbb{R}^2$到图像$f(M) \subset \mathbb{R^3}$时如何拉伸正切向量。顺便提一下，对于上面的图像，我们可以更精确一点并且用极限项定义$df(X)$：

$df_p(X) = \lim_{h \rightarrow 0} \frac{f(p + hX) - f(p)}{h}$

这个公式仍然有一点抽象——我们可能想要一些更明确东西去在实际中使用。当我们开始在离散曲面上操作时，我们将看到$df(X)$通常有极其明确的意义——比如，它可能与我们三角网格的一条边对应。但是在平滑设定中$df$的一个更典型的表达是雅可比矩阵

$\mathsf{J} = \begin{bmatrix} \partial f^1/ \partial x^1 & \partial f^1/ \partial x^2 \\ \partial f^2/ \partial x^1 & \partial f^2/ \partial x^2 \\ \partial f^3/ \partial x^1 & \partial f^3/ \partial x^2 \end{bmatrix}$

这里我们选取$\mathbb{R}^2$和$\mathbb{R}^3$上的坐标系，然后想象对于一些标量函数$f_1,f_2,f_3:M \rightarrow \mathbb{R}$的元组有

$f(x^1, x^2) = (f_1(x^1,x^2), f_2(x^1,x^2), f_3(x^1,x^2))$

所以如果你想要计算$df(X)$，你可以简单的将$J$作用到一些向量$X = [X^1, X^2]^T$上。

被认为有害的坐标系表示

你可能早就得到了上面方法的一个反馈：写出来的表达式变得更长更复杂了。但是有其它的好理由去拒绝明确的矩阵表示。最强烈的理由是矩阵可以被用来表示非常多不同种类的目标，并且这些对象可以用非常不同的方式表示。比如，你能猜猜下面这个矩阵表示什么吗？

$\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}$

放弃了？它的确十分明确：它是一个两个顶点上完全图的邻接矩阵。不，等一下——它应该是一个Puali矩阵$\sigma_x$，表示沿着$x$轴的旋转角动量。或者这个矩阵表示二面体群$D_4$的一个元素？你获得了这样一个想法：当使用矩阵的时候，很容易忘记它们到底是从哪里来的——这让它非常容易遗忘它们应该遵守的规则！（难道你不是早就有了足够多不想丢掉的东西吗？）这里有一个真实的哲学观点是矩阵不是对象：它们只不过是对象的表示！或者改变一些柏拉图说的话：矩阵仅仅是洞穴中墙壁上的阴影，它除了我们想要去照亮的真实对象的黑暗印象以外什么也不能提供。

一个更具体的例子经常在几何学中出现，是线性算子和双线性型的区别。注意一下，线性算子是从一个向量空间到另一个向量空间的映射，即

$f:\mathbb{R}^2 \rightarrow \mathbb{R}^2;u \mapsto f(u)$

而双线性型是从一对向量到一个标量的映射，即

$\mathsf{g} : \mathbb{R}^2 \times \mathbb{R}^2 \rightarrow \mathbb{R};(u,v) \mapsto \mathsf{g}(u,v)$

放上这两个例子让我们想象我们正在一个坐标系统$(x^1,x^2)$上操作，其中$f$和$\mathsf{g}$由矩阵$\mathsf{A},\mathsf{B}\in \mathbb{R}^{2 \times 2}$表示，并且它们的参数由向量$\mathsf{u},\mathsf{v} \in \mathbb{R}^2$表示。换句话说，我们有

$f(u) = \mathsf{Au}$

和

$\mathsf{g}(u,v) = \mathsf{u^TBv}$

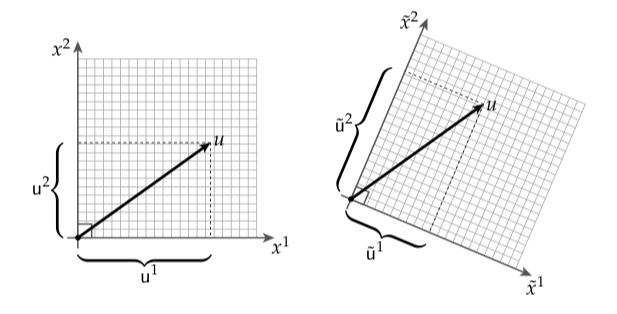
现在假设我们需要在不同的坐标系$(\tilde{x}^1,\tilde{x}^2)$中工作，同过基变换$\mathsf{P} \in \mathbb{R}^{2 \times 2}$与第一个联系起来。比如，向量$u$和$v$通过下式进行变换

$\begin{aligned} \mathsf{\tilde{u}} &= \mathsf{Pu} \\ \mathsf{\tilde{v}} &= \mathsf{Pv} \end{aligned}$

我们如何在新的坐标系统中表示映射$f$和$\mathsf{g}$？比如我们不能简单的计算$\mathsf{A\tilde{u}}$，由于$\mathsf{A}$和$\mathsf{\tilde{u}}$在不同的坐标系统中表示。我们需要去做的是计算

$f(u) = \mathsf{PAu} = \mathsf{PAP}^{-1}\mathsf{\tilde{u}}$

和类似的

$\mathsf{g}(u,v) = \mathsf{u^TBv} = \mathsf{(P^{-1}\tilde{u})^T B (P^{-1}\tilde{v})} = \mathsf{\tilde{u}^T (P^{-T}BP^{-T}) \tilde{v}}$

换句话说，线性算子变成了

$\mathsf{A \mapsto PAP^{-1}}$

而双线性型变为

$\mathsf{B \mapsto P^{-T} B P^{-T}}$

所以我们发现了并不是所有的矩阵以同样的方式变换！但是如果我们不断地涂画一些数字的格子，将会非常容易丢失那些应该被作用在对象上的变换。

曲面几何中的标准矩阵

关于刚刚坐标系的告诫，它非常有用地让我们意识到对于几何对象的标准矩阵表示，因为它们给传统结果提供了一个基本联系。我们早就已经看过了对于一个对象的矩阵表示：微分$df$可以被编码称包含浸入$f$一阶导数的雅可比矩阵$\mathsf{J}$。关于其它的我们在曲面学习中遇到的对象呢？引导度量$\mathsf{g}$被相当容易的指出，因为它仅仅是一个微分的函数——记住

$\mathsf{g}(u,v) = df(u) \cdot df(v)$

等价地，如果我们使用一个矩阵$I \in \mathbb{R}^{2 \times 2}$来表示$\mathsf{g}$，那么我们有

$\mathsf{u^T} I \mathsf{v = (Ju)^T (Jv)}$

这意味着

$I = \mathsf{J^TJ}$

我们使用字母“$I$”表示引导度量的矩阵，它在历史上被用来表示第一基本型——今天更少的作者使用这个术语了。在微分几何更古老的书里面你可能也能看到人们讨论“$\mathsf{E}$”，“$\mathsf{F}$”和“$\mathsf{G}$”，它们分别表示$I$中特定的元素：

$I = \begin{bmatrix} \mathsf{E} & \mathsf{F} \\ \mathsf{F} & \mathsf{G} \end{bmatrix}$

（能明确为什么“$\mathsf{F}$”出现两次吗？）你可能猜想字母表中第五个、第六个和第七个字母已经完全过时了，因为它们是如此坐标有关的，因此它们自己几乎不带有几何意义。不过，能够意识到这些生物是有用的，因为它们确实在野外出现。

早些时候，我们有提到形状算子，被定义为单射$\mathcal{S}:TM \rightarrow TM$，其满足

$dN(X) = df(SX)$

并且第二基本型被定义为

$II(u,v) = \mathsf{g}(\mathcal{S}u,v)$

（记住相对于$\mathsf{g}$来说$\mathcal{S}$是自共轭的，并且同样地，$II$相对于它的参数$u$和$v$来说是对称的。）如果我们让$\mathsf{S,II}\in \mathbb{R}^{2\times 2}$分别成为$\mathcal{S}$和$II$的矩阵表示，那么对于所有的向量$\mathsf{u,v} \in \mathbb{R}^3$我们有

$\mathsf{u^T II v = u^T I S v}$

或者等价地

$\mathsf{II = IS}$

$\mathsf{II}$中的元素传统上会和罗马字母表中的小写字母联系起来，记为

$\mathsf{II} = \begin{bmatrix} \mathsf{e} & \mathsf{f} \\ \mathsf{f} & \mathsf{g} \end{bmatrix}$

在坐标系$(x,y)$中将具体表示为（这个内容的推导这里应该是超出了这个文档的范围，如果有谁可以通过这个文档中的内容推导出来的话请告诉我）

$\begin{aligned} \mathsf{e} &= N \cdot f_{xx} \\ \mathsf{f} &= N \cdot f_{xy} \\ \mathsf{g} &= N \cdot f_{yy} \end{aligned}$

其中$N$是单位曲面法线，并且$f_{xy}$表示沿着$x$和$y$方向的二阶偏导。

此时我们可能想停下来并且询问：像$\mathsf{IS}$这样的矩阵表示的变换和基变换比较怎么样呢？第一项，$\mathsf{I}$，是一个双线性型，但是第二项$\mathsf{S}$是一个线性映射！就像上面强调的一样，我们不能仅仅通过关注矩阵本身确定答案——我们需要意识到它们到底表示什么。在这个情况下，我们知道$\mathsf{IS}$对应第二基本型，所以它应该像其它的双线性型一样变换：$\mathsf{IS} \mapsto \mathsf{P^{-1}} IS \mathsf{P^{-1}}$

最后，我们可以验证使用矩阵的古典几何表示和我们之前使用微分的表示对应。比如，法线曲率的古典表示为

$\kappa_n(u) = \frac{II(u,u)}{I(u,u)}$

我们可以将它重写为

$\frac{\mathsf{u^T II u}}{\mathsf{u^T I u}} = \frac{\mathsf{u^T IS u}}{\mathsf{u^T Iu}} = \frac{\mathsf{(Ju)^T(JSu)}}{\mathsf{(Ju)^T(Ju)}} = \frac{df(u) \cdot dN(u)}{|df(u)|^2}$

直到符号的选择，这个表达式和我们之前通过考虑嵌入在曲面中的曲线得到的表达式一样。