泊松重建

开源项目地址

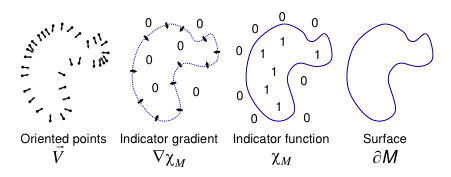
基本思想

目的是计算3D指示函数（indicator function）$\mathcal{X}$，$\mathcal{X}$是一个泛函，将曲面外的点映射为$0$，将曲面内的点映射为$1$。

解决问题的关键依据是：模型曲面的有向采样点与模型指示函数之间存在积分的关系。

使用$\min_\mathcal{X} \| \nabla \mathcal{X} - \vec{V} \|$，找到合适的函数$\mathcal{X}$使得其梯度最贴近由采样点定义的向量场$\vec{V}$。在此基础上应用散度，将这个变分问题转换为一个标准泊松问题：

$\Delta \mathcal{X} = \nabla \cdot \nabla \mathcal{X} = \nabla \cdot \vec{V}$

泊松重建方法是一个全局求解的方法，一次性考虑所有的点。

系统概览

输入： 曲面采样集合$s \in S$，其中每一个元素都包含坐标$s.p$和向内法线$s.\vec{N}$；并假设这些点都在模型$M$的曲面$\partial M$上，或者离曲面很近。

输出：模型$M$对应的指示函数$\mathcal{X}$，并提取等值面（isosurface）作为曲面。

挑战：从采样点精确计算$\mathcal{X}$

具体思路

由于指示函数成片的都是常数（在模型外全是0，在模型内全是1），梯度场的计算可能导致在曲面边界处存在没有边界的值（unbounded value）。为了拒绝这种情况发生，将指示函数与平滑滤波器卷积并考虑卷积后函数的梯度场。

引理：给定带边界的立体模型$M$，令$\mathcal{X}_M$表示$M$的指示函数，$\vec{N}_{\partial M}(p)$为$p \in \partial M$处的向内曲面法线，$\tilde{F}(q)$为平滑滤波器，并且$\tilde{F}_p(q) = \tilde{F}(q-p)$将它转移到点$p$处。平滑后指示函数的梯度等于由平滑曲面法线场获得的向量：

$\nabla (\mathcal{X}_M * \tilde{F})(q_0) = \intop_{\partial M} \tilde{F}_p(q_0) \vec{N}_{\partial M}(p) dp$

（原文中有证明）

由于不知道曲面几何，因此不能计算曲面积分；但是输出的有向点集提供了足够的信息去使用离散求和估计积分。

使用点集$S$将$\partial M$划分为独立的块（patch）$\mathscr{P}_s \subset \partial M$，在独立的块上使用采样点坐标$s.p$估计在块$\mathscr{P}_s$上的积分，通过块的面积尺度化（每个块的求和权重）：

$\begin{aligned} \nabla (\mathcal{X}_m * \tilde{F})(q) &= \sum_{s \in S} \intop_{\mathscr{P}_s} \tilde{F}_p(q) \vec{N}_{\partial M}(p)dp \\ &\approx \sum_{s \in S} | \mathscr{P}_s | \tilde{F}_{s.p}(q) s.\vec{N} \equiv \vec{V}(q) \end{aligned}$

虽然任意的平滑滤波器$\tilde{F}$理论上都可行，但是实际上需要慎重选择，最好能满足以下两个条件：

1. 足够窄，不至于过平滑（over-smooth）
2. 足够宽，可以很好的通过由块面积尺度化的在$s.p$处的值估计$\mathscr{P}_s$上的积分

因此选择高斯滤波器，其方差与分辨率相关。

求解 $\nabla \tilde{\mathcal{X}} = \vec{V}$，然而$\vec{V}$一般是不可积的，所以解析解一般不存在。为了更好的估计最小二乘解，在这个等式上应用散度算子得到一个泊松方程

$\Delta \tilde{\mathcal{X}} = \nabla \cdot \vec{V}$

实现

定义了空间函数在曲面附近有高分辨率，远离曲面有低分辨率（八叉树）；向量场$\vec{V}$由空间中一些函数的线性和表示；设置并求解泊松方程；提取指数函数等值面。

离散化

必须选择函数空间去离散化这个问题。使用均匀分辨率的结果开销太大，因此使用八叉树（octree）。

使用采样点的位置定义八叉树$\mathscr{O}$并且将函数$F_o$与树的每个节点$o \in \mathscr{O}$关联，选择的树和函数需要满足以下条件：

1. 向量场$\vec{V}$可以用$F_o$的线性和精准有效地表示
2. 由$F_o$项表示的泊松方程矩阵形式可以被有效求解
3. 指示函数作为$F_o$和的形式可以在模型曲面附近被精准有效地估计

定义函数空间

给定采样点集$S$和最大树深度$D$，定义八叉树$\mathscr{O}$为满足每个采样点都落到深度$D$的叶节点上的最小八叉树。

定义一个函数空间，由一个固定的、单位积分的（unit-intergral）基函数$F: \mathbb{R}^3 \rightarrow \mathbb{R}$的平移和缩放张成。对于每个节点$o \in \mathscr{O}$，设$F_o$为以$o$为中心且由$o$的尺寸拉伸的单位积分“节点函数”：

$F_o(q) \equiv F \left( \frac{q - o.c}{o.w} \right) \frac{1}{o.w^3}$

其中$o.c$和$o.w$分别是节点$o$的中心和宽。

函数空间$\mathscr{F}_{\mathscr{O}, F} \equiv \text{Span}\{ F_o \}$有多分辨率结构，类似于传统的小波表示。越好的节点对应越高频的函数，离曲面越近函数表示越精确。

选择基函数

在选择基函数$F$中，目的是选择一个函数，使得向量场$\vec{V}$可以由节点函数$\{ F_o \}$的线性和精确有效地表示。

如果将每个采样点的坐标替换为包含它的叶节点中心，向量场$\vec{V}$可以由$\{ F_o \}$的线性和有效地表示：

$F(q) = \tilde{F} \left( \frac{q}{2^D} \right)$

这样每一个采样点都贡献了一项（法向量）到对应它的叶子的节点函数的系数。

由于最大树深度$D$对应$2^{-D}$的采样宽度，平滑滤波器应该近似为方差在$2^{-D}$阶上的高斯。因此$F$一个近似为单位方差的高斯。

为了效率我们通过一个简洁的支持函数近似一个单位方差的高斯，因此有：

1. 得到的散度和拉普拉斯算子是稀疏的
2. 估计在点$q$处表示为$F_o$线性和的函数，仅仅需要将在$q$比较近的节点$o \in \mathscr{O}$上求和。

设置$F$为盒滤波器（box filter）与自己的第$n$次卷积，得到的基函数$F$：

$F(x,y,z) \equiv (B(x)B(y)B(z))^{*n} ~~ \text{with} ~~ B(t) = \begin{cases} 1 & |t| < 0.5 \\ 0 & \text{otherwise} \end{cases}$

当$n$增长的时候，$F$更接近高斯并且支持范围更大；在该文的实际实现中使用$n=3$。

向量场定义

为了获得亚节点精度，该方法拒绝将采样点的坐标放在包含它的叶节点中心，而是在8个最邻近节点间使用三线性内插。因此，将指示函数的梯度场近似定义为：

$\vec{V}(q) \equiv \sum_{s \in S} \sum_{o \in \text{Ngbr}_D(s)} \alpha_{o,s} F_o(q) s.\vec{N}$

其中$\text{Ngbr}_D(s)$是与$s.p$最近的8个深度D的节点，$\{ \alpha_{o,s} \}$是三线性内插权重。

这里先假设采样是均匀的（后面有对不均匀采样的说明），假设块$\mathscr{P}_s$的面积是常数并且$\vec{V}$是在一个数乘差别下对平滑指示函数的梯度很好的近似。

泊松求解

在定义了向量场$\vec{V}$之后，就可以开始求解函数$\tilde{\mathcal{X}} \in \mathscr{F}_{\mathscr{O},F}$使得$\tilde{\mathcal{X}}$的梯度更接近$\vec{V}$，即泊松方程$\Delta \tilde{\mathcal{X}} = \nabla\cdot \vec{V}$。

求解$\tilde{\mathcal{X}}$的一个挑战是虽然函数$\tilde{\mathcal{X}}$和$\vec{V}$的坐标函数在空间$\mathscr{F}_{\mathscr{O},F}$中，但是函数$\Delta \tilde{\mathcal{X}}$和$\nabla \cdot \vec{V}$却不是必须的。

求解函数$\tilde{\mathcal{X}}$使得$\Delta \tilde{\mathcal{X}}$在空间$\mathscr{F}_{\mathscr{O},F}$上的投影和$\nabla \cdot \vec{V}$的投影最近。由于函数$F_o$在一般情况下不是有正交基构造的，之间求解这个问题会变得特别没有效率。将这个问题简化为求解函数$\tilde{\mathcal{X}}$最小化：

$\sum_{o \in \mathscr{O}} \| \langle \Delta \tilde{\mathcal{X}} - \nabla \cdot \vec{V}, F_o \rangle \|^2 = \sum_{o \in \mathscr{O}} \| \langle \Delta \tilde{\mathcal{X}}, F_o \rangle - \langle \nabla \cdot \vec{V}, F_o \rangle \|^2$

给定第$o$个坐标为$v_o = \langle \nabla \cdot \vec{V}, F_o \rangle$的$|\mathscr{O}|$维向量$v$，目标是求解函数$\tilde{\mathcal{X}}$使得$\tilde{\mathcal{X}}$的拉普拉斯在每一个$F_o$上的投影都尽可能接近$v$。

为了写成矩阵形式，令$\tilde{\mathcal{X}} = \sum_o x_o F_o$，因此是在求解向量$x \in \mathbb{R}^{|\mathscr{O}|}$。然后定义$|\mathscr{O}| \times |\mathscr{O}|$矩阵$L$使得$Lx$返回拉普拉斯和每个$F_o$的点积。对于所有的$o, o' \in \mathscr{O}$，$L$中$(o, o')$元素为：

$L_{o,o'} \equiv \langle \frac{\partial^2 F_o}{\partial x^2}, F_{o'} \rangle + \langle \frac{\partial^2 F_o}{\partial y^2}, F_{o'} \rangle + \langle \frac{\partial^2 F_o}{\partial z^2}, F_{o'} \rangle$

求解$\tilde{\mathcal{X}}$等价于

$\min_{x \in \mathbb{R}^{|\mathscr{O}|}} \| Lx - v \|^2$

矩阵$L$是稀疏且对称的。（稀疏是因为$F_o$是局部的，对称是因为$\intop f''g = - \intop f'g'$）

等值面提取

为了获得重建的曲面$\partial \tilde{M}$，必须首先选取等值面对应的值并且从计算得到的指示函数中提取对应的等值面。

选择这个值使得提取的曲面近似输入采样点的位置。通过估计采样点处的$\tilde{\mathcal{X}}$并计算平均值用以提取等值面：

$\partial \tilde{M} \equiv \{ q \in \mathbb{R}^3 | \tilde{\mathcal{X}}(q) = \gamma \} ~~ \text{with} ~~ \gamma = \frac{1}{|S|} \sum_{s \in S} \tilde{\mathcal{X}} (s.p)$

这个选择有一个好处是$\tilde{\mathcal{X}}$的尺度缩放不会改变等值面。（向量场定义有提到一个数乘的差别）

非均匀采样

前面的推导是在均匀采样假设下的。

估计局部采样密度

给定深度$\hat{D} \le D$设置深度估计器为在深度$\hat{D}$处节点函数的和：

$W_{\hat{D}}(q) \equiv \sum_{s \in S} \sum_{o \in \text{Ngbr}_{\hat{D}}(s)} \alpha_{o,s}F_o(q)$

计算向量场

每一个采样点的贡献和它在曲面上对应的面积是相关的。面积跟采样密度逆相关：

$\vec{V}(q) \equiv \sum_{s \in S} \frac{1}{W_{\hat{D}} (s.p)} \sum_{o \in \text{Ngbr}_D(s)} \alpha_{o,s} F_o(q) s.\vec{N}$

只适应采样点贡献大小在稀疏采样区域会导致很差的噪声平滑。因此针对局部采样密度增加适应平滑滤波器$\tilde{F}$的宽度。

由于深度更小的节点函数对应更宽的平滑滤波器，定义

$\vec{V}(q) \equiv \sum_{s \in S} \frac{1}{W_{\hat{D}} (s.p)} \sum_{o \in \text{Ngbr}_{\text{Depth}(s.p)}(s)} \alpha_{o,s} F_o(q) s.\vec{N}$

在这个定义中，$\text{Depth}(s.p)$表示采样点$s \in S$希望的深度。被定义为在所有采样点上计算平均采样密度$W$

$\text{Depth}(s.p) \equiv \min (D, D + \log_4(W_{\hat{D}} (s.p) / W))$

平滑滤波器的宽度和相关的曲面块$P_s$的半径相关。

选取提取等值面的值

$\tilde{\mathcal{X}}$在采样点处的加权平均值：

$\partial \tilde{M} \equiv \{ q \in \mathbb{R}^3 | \tilde{\mathcal{X}}(q) = \gamma \} ~~ \text{with} ~~ \gamma = \frac{\sum \frac{1}{W_{\hat{D}}(s.p)} \tilde{\mathcal{X}}(s.p)}{\sum \frac{1}{W_{\hat{D}}(s.p)}}$