Laplacian on Triangle Mesh | HyperPlane

Laplacian on Triangle Mesh

发表于 | 更新于 | 阅读次数：

图形学中经常会涉及到拉普拉斯算子，在这里介绍一下拉普拉斯算子在三角mesh上的具体实现。

预备内容

在真正开始讨论拉普拉斯算子之前，我们先说明一些预备的知识。

局部平均区域

基本思想是将计算微分性质作为mesh上点x\mathbf{x}局部邻域N(x)\mathcal{N}(\mathbf{x})上的空间平均。下图是几种具体情况：
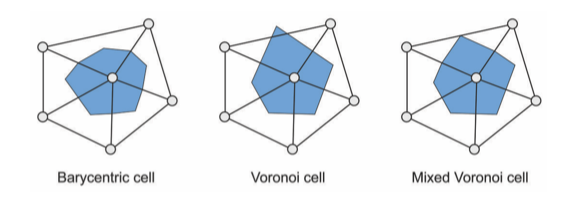
region

图中的蓝色区域为局部平均区域。其中barycentric cell是将三角形的重心和三角形边的中点相连，Voronoi cell是将重心换成了外心。使用外心有一个问题，对于钝角三角形来说外心在三角形外部，因此mixed Voronoi cell将钝角三角形的外心替换为钝角对边的中点。

梯度

由于拉普拉斯算子是梯度的散度，所以梯度也是很重要的。假设一个由每个mesh顶点定义的逐块线性函数ff，f(vi)=f(xi)=f(ui)=fif(v_i) = f(\mathbf{x}_i) = f(\mathbf{u}_i) = f_i，内插得到每一个三角形(xi,xj,xk)(\mathbf{x}_i, \mathbf{x}_j, \mathbf{x}_k)：

f(u)=fiBi(u)+fjBj(u)+fkBk(u)f(\mathbf{u}) = f_iB_i(\mathbf{u}) + f_jB_j(\mathbf{u}) + f_kB_k(\mathbf{u})

其中u\mathbf{u}是x\mathbf{x}在2D共形参数化上的对应参数。内插效果为：
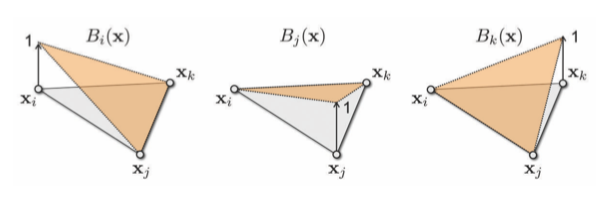
Gradients

那么ff的梯度为

∇f(u)=fi∇Bi(u)+fj∇Bj(u)+fk∇Bk(u)\nabla f(\mathbf{u}) = f_i \nabla B_i(\mathbf{u}) + f_j \nabla B_j(\mathbf{u}) + f_k \nabla B_k(\mathbf{u})

由于是线性插值，我们有条件对于所有的u\mathbf{u}我们有Bi(u)+Bj(u)+Bk(u)=1B_i(\mathbf{u}) + B_j(\mathbf{u}) + B_k(\mathbf{u}) = 1，因此∇Bi(u)+∇Bj(u)+∇Bk(u)=0\nabla B_i(\mathbf{u}) + \nabla B_j(\mathbf{u}) + \nabla B_k(\mathbf{u}) = 0。联合上面的式子我们可以得到：

∇f(u)=(fj−fi)∇Bj(u)+(fk−fi)∇Bk(u)\nabla f(\mathbf{u}) = (f_j - f_i) \nabla B_j(\mathbf{u}) + (f_k - f_i) \nabla B_k(\mathbf{u})

这个函数的最速上升方向是垂直于顶点对边的方向，再加上合适的归一化，有

∇Bi(u)=(xk−xj)⊥2AT\nabla B_i (\mathbf{u}) = \frac{(\mathbf{x}_k - \mathbf{x}_j)^{\perp}}{2A_T}

其中⊥\perp表示逆时针旋转90度，ATA_T表示三角形TT的面积。那么在三角形中每一点的梯度为常数：

∇f(u)=(fj−fi)(xi−xk)⊥2AT+(fk−fi)(xj−xi)⊥2AT\nabla f(\mathbf{u}) = (f_j - f_i) \frac{(\mathbf{x}_i - \mathbf{x}_k)^{\perp}}{2A_T} + (f_k - f_i) \frac{(\mathbf{x}_j - \mathbf{x}_i)^{\perp}}{2A_T}

离散拉普拉斯算子

预备内容说完了开始讲讲主题了

均匀拉普拉斯

拉普拉斯算子的均匀离散版本

Δf(vi)=1∣N1(vi)∣∑vj∈N1(vi)(fj−fi)\Delta f(v_i) = \frac{1}{|\mathcal{N}_1(v_i)|} \sum_{v_j \in \mathcal{N}_1(v_i)} (f_j - f_i)

总的来说，这个形式用处不大。但是也可以用在各向同性的remesh上。

余切公式

使用混合的有限元/有限体方法（mixed finite element/finite volume method），拉普拉斯算子可以有更精确的离散推导。目标是在局部平均域Ai=A(vi)A_i = A(v_i)上，对逐片线性函数梯度的散度进行积分。为了简化这个积分，对向量值函数F\mathbf{F}的积分应用散度定理：

∫AidivF(u)dA=∫∂AiF(u)⋅n(u)ds\intop_{A_i} \text{div} \mathbf{F}(\mathbf{u}) \text{d}A = \intop_{\partial A_i} \mathbf{F}(\mathbf{u}) \cdot \mathbf{n}(\mathbf{u}) \text{d}s

这个等式将面积AiA_i上的积分转换为了在AiA_i边界∂Ai\partial A_i上的积分，其中n\mathbf{n}是边界向外的单位法线。
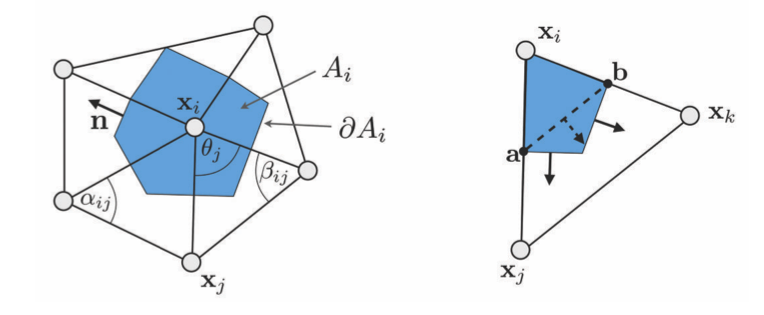
Gradients

将拉普拉斯应用到散度定理中

∫AiΔf(u)dA=∫Aidiv∇f(u)dA=∫∂Ai∇f(u)⋅n(u)ds\intop_{A_i} \Delta f(\mathbf{u}) \text{d}A = \intop_{A_i} \text{div} \nabla f(\mathbf{u}) \text{d}A = \intop_{\partial A_i} \nabla f(\mathbf{u})\cdot \mathbf{n}(\mathbf{u})\text{d}s

将积分分解到每个三角形上。由于局部的Voronoi区域通过三角形两条边的中点a\mathbf{a}和b\mathbf{b}，并且每个三角形中∇f(x)\nabla f(\mathbf{x})是常数，那么在该三角形TT上的积分为

∫∂Ai∩T∇f(u)⋅n(u)ds=∇f(u)⋅(a−b)⊥=12∇f(u)⋅(xj−xk)⊥\begin{aligned} \intop_{\partial A_i \cap T} \nabla f(\mathbf{u}) \cdot \mathbf{n}(\mathbf{u}) \text{d}s &= \nabla f(\mathbf{u}) \cdot (\mathbf{a} - \mathbf{b})^{\perp} \\ &= \frac{1}{2} \nabla f(\mathbf{u}) \cdot (\mathbf{x}_j - \mathbf{x}_k)^{\perp} \end{aligned}

然后我们将上面得到的梯度离散化公式带进来，得到

∫∂Ai∩T∇f(u)⋅n(u)ds=(fj−fi)(xi−xk)⊥⋅xj−xk)⊥4AT+(fk−fi)(xj−xi)⊥⋅xj−xk)⊥4AT\begin{aligned} \intop_{\partial A_i \cap T} \nabla f(\mathbf{u}) \cdot \mathbf{n}(\mathbf{u}) \text{d}s &= (f_j - f_i)\frac{(\mathbf{x}_i - \mathbf{x}_k)^{\perp} \cdot \mathbf{x}_j - \mathbf{x}_k)^{\perp}}{4A_T} \\ &+ (f_k - f_i)\frac{(\mathbf{x}_j - \mathbf{x}_i)^{\perp} \cdot \mathbf{x}_j - \mathbf{x}_k)^{\perp}}{4A_T} \end{aligned}

激动人心的部分要来了！赶快会议一下各种三角公式！

让γj\gamma_j和γk\gamma_k分别表示顶点vjv_j和vkv_k的三角形内角。由于有

AT=12sin⁡γj∥xj−xi∥∥xj−xk∥=12sin⁡γk∥xi−xk∥∥xj−xk∥A_T = \frac{1}{2} \sin \gamma_j \| \mathbf{x}_j - \mathbf{x}_i \| \| \mathbf{x}_j - \mathbf{x}_k \| = \frac{1}{2} \sin \gamma_k \| \mathbf{x}_i - \mathbf{x}_k \| \| \mathbf{x}_j - \mathbf{x}_k \|

并且有

cos⁡γj=(xj−xi)⋅(xj−xk)∥xj−xi∥∥xj−xk∥cos⁡γk=(xi−xk)⋅(xj−xk)∥xi−xk∥∥xj−xk∥\begin{aligned} \cos \gamma_j &= \frac{( \mathbf{x}_j - \mathbf{x}_i ) \cdot ( \mathbf{x}_j - \mathbf{x}_k )}{\| \mathbf{x}_j - \mathbf{x}_i \|\| \mathbf{x}_j - \mathbf{x}_k \|} \\ \cos \gamma_k &= \frac{( \mathbf{x}_i - \mathbf{x}_k ) \cdot ( \mathbf{x}_j - \mathbf{x}_k )}{\| \mathbf{x}_i - \mathbf{x}_k \|\| \mathbf{x}_j - \mathbf{x}_k \|} \end{aligned}

于是就可以得到

∫∂Ai∩T∇f(u)⋅n(u)ds=12(cot⁡γk(fj−fi)+cot⁡γj(fk−fi))\intop_{\partial A_i \cap T} \nabla f(\mathbf{u}) \cdot \mathbf{n}(\mathbf{u}) \text{d}s = \frac{1}{2} (\cot \gamma_k (f_j - f_i) + \cot \gamma_j (f_k - f_i))

因此在整个局部平均区域AiA_i上积分的时候会得到

∫AiΔf(u)dA=12∑vj∈Ni(vi)(cot⁡αi,j+cot⁡βi,j)(fi−fj)\intop_{A_i} \Delta f(\mathbf{u}) \text{d}A = \frac{1}{2} \sum_{v_j \in \mathcal{N}_i(v_i)} (\cot \alpha_{i,j} + \cot \beta_{i,j})(f_i - f_j)

αi,j\alpha_{i,j}，βi,j\beta_{i,j}与xi\mathbf{x}_i，xj\mathbf{x}_j的位置关系在上图有给出。

于是，在顶点viv_i处，函数ff的拉普拉斯算子的离散平均为

Δf(u):=12Ai∑vj∈Ni(vi)(cot⁡αi,j+cot⁡βi,j)(fi−fj)\Delta f(\mathbf{u}) \coloneqq \frac{1}{2 A_i} \sum_{v_j \in \mathcal{N}_i(v_i)} (\cot \alpha_{i,j} + \cot \beta_{i,j})(f_i - f_j)

这就是在计算机图形学中大名鼎鼎的余切公式了。

矩阵化求解

如果要求解肯定还是要具体写成矩阵形式的线性方程，接下来就介绍如何矩阵化一个拉普拉斯或者泊松方程。

矩阵化

考虑在三角mesh上的泊松方程Δf=b\Delta f = b或者更高阶偏微分方程Δkf=b\Delta^k f = b的离散化及求解。标量值函数f:S→Rf:\mathcal{S} \rightarrow \mathbb{R}是通过在mesh顶点viv_i处的函数值fi=f(vi)f_i = f(v_i)的逐片线性内插定义的。从上面的推导我们知道了拉普拉斯Δf\Delta f可以写成线性求和的形式

Δf(vi)=wi∑vj∈N1(vi)wij(f(vj)−f(vi))\Delta f(v_i) = w_i \sum_{v_j \in \mathcal{N}_1(v_i)} w_{ij} (f(v_j) - f(v_i))

如果使用余切离散化那么就是wi=12Aiw_i = \frac{1}{2 A_i}，wij=(cot⁡αi,j+cot⁡βi,j)w_{ij} = (\cot \alpha_{i,j} + \cot \beta_{i,j})。将线性和写成矩阵形式之后，我们有

(Δf(v1)⋮Δf(vn))=DM⎵L(f(v1)⋮f(vn))\begin{pmatrix} \Delta f(v_1) \\ \vdots \\ \Delta f(v_n) \end{pmatrix}=\underbrace{DM}_L \begin{pmatrix} f(v_1) \\ \vdots \\ f(v_n) \end{pmatrix}

其中D=diag(w1,…,wn)\mathbf{D} = \text{diag} (w_1, \dots, w_n)，M\mathbf{M}是对称矩阵

mi,j={−∑vk∈N1(vi)wik,i=jwij,vj∈Ni(vi)0,otherwisem_{i,j} = \begin{cases} -\sum_{v_k \in \mathcal{N}_1(v_i)} w_{ik}, &i = j \\ w_{ij}, &v_j \in \mathcal{N}_i(v_i) \\ 0, & \text{otherwise} \end{cases}

更高阶的拉普拉斯可以通过递归的方法得到

Δkf(vi)=wi∑vj∈N1(vi)wij(Δk−1f(vj)−Δk−1f(vi))\Delta^k f(v_i) = w_i \sum_{v_j \in \mathcal{N}_1(v_i)} w_{ij} ( \Delta^{k-1} f(v_j) - \Delta^{k-1} f(v_i))

那么这个矩阵表示就很简单的对应拉普拉斯矩阵L\mathbf{L}的k次幂Lk=(DM)k\mathbf{L}^k = (\mathbf{DM})^k。

因此在nn个顶点的mesh上更高阶的偏微分方程Δkf=b\Delta^k f = b离散化之后会得到一个(n×n)(n \times n)的线性系统

Lkx=b\mathbf{L}^k \mathbf{x} = \mathbf{b}

其中x=(f(v1),…,f(vn))T\mathbf{x} = (f(v_1), \dots, f(v_n))^T，且b=(b(v1),…,b(vn))T\mathbf{b} = (b(v_1), \dots, b(v_n))^T

矩阵性质

你以为上面就结束了吗？还没有呢！为了保证二次型的对称正定，还需要对上面推导出来的内容进一步调整。

稀疏性 简单说一下吧。拉普拉斯矩阵中只有对角元和边对应的元素是非00的，其余全是0。根据欧拉公式，平均每一行大约7个非00元素。

对称性 由于对角矩阵D\mathbf{D}捣乱，所以矩阵L=DM\mathbf{L} = \mathbf{DM}不是对称的。不过对于任意kk阶的拉普拉斯系统很容易转换为对称系统，即

M(DM)k−1x=D−1b\mathbf{M} (\mathbf{DM})^{k-1} \mathbf{x} = \mathbf{D}^{-1} \mathbf{b}

这个对称性应该很容易验证了。

正定性 一般来讲，解偏微分方程都需要边界条件。即对于一个线性系统Ax=b\mathbf{Ax = b}，有部分变量xix_i保持不变，此时它们不再是未知量了。此时将对应的列ai\mathbf{a}_i移到右手边，即b←b−xiai\mathbf{b} \leftarrow \mathbf{b} - x_i\mathbf{a}_i，同时对应的行从整个系统中移除。注意到此时整个系统还是保持对称的！！！在移除边界条件之后，可以证明矩阵L\mathbf{L}是负定的！（简单点理解，有些行中对角元的绝对值大于该行其它列的元素绝对值的和。请注意，这只是直观理解，绝不是严格证明！！！）负定很简单，直接在每个L\mathbf{L}上乘一个−1-1就行，因此我们最后得到

(−1)kM(DM)k−1x=(−1)kD−1b(-1)^k \mathbf{M} (\mathbf{DM})^{k-1} \mathbf{x} = (-1)^k \mathbf{D}^{-1} \mathbf{b}

由此我们就得到了一个稀疏、对称且正定的线性系统。

参考文献

  • M. Botsch, Ed., Polygon mesh processing. Natick, Mass: A K Peters, 2010.